Estou estudando pra uma prova e um dos assuntos será trigonometria, tenho que treinar muito!
Gostaria que alguém conferisse se resolvi o seguinte exercício corretamente e se dá pra simplificar mais ainda a resposta final.
(Agora com o editor de fórumla
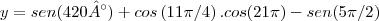
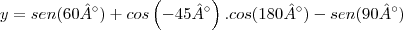
![y= \frac{\sqrt[]{3}}{2}+\left(-\frac{\sqrt[]{2}}{2} \right) . [-1 -1] y= \frac{\sqrt[]{3}}{2}+\left(-\frac{\sqrt[]{2}}{2} \right) . [-1 -1]](/latexrender/pictures/0166dfa8c49bc08296a3f627e162f491.png)
![y= \frac{\sqrt[]{3}-\sqrt[]{2}}{2} . \left(-2 \right) y= \frac{\sqrt[]{3}-\sqrt[]{2}}{2} . \left(-2 \right)](/latexrender/pictures/6fc6cd5d48e3457ebfbeb0d3d28981da.png)
![y= \frac{-2\left(\sqrt[]{3}-\sqrt[]{2} \right)}{2} y= \frac{-2\left(\sqrt[]{3}-\sqrt[]{2} \right)}{2}](/latexrender/pictures/eeaea8ef27f8875a206faf4a9d8c45ab.png)
E aí tudo certinho? Será que agora posso cortar o 2 de cima com o de baixo? Aí vai ficar -raiz de 3 + raiz de 2?
Vlw!!


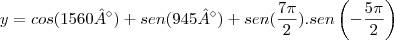
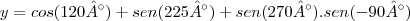
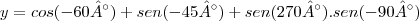
![y = -\frac{1}{2}+\left(-\frac{\sqrt[]{2}}{2} \right)-1.(-1) y = -\frac{1}{2}+\left(-\frac{\sqrt[]{2}}{2} \right)-1.(-1)](/latexrender/pictures/9c19f076ecc190b1de48880027f568dc.png)
![y = (\frac{-1-\sqrt[]{2}}{2}+1).-1 y = (\frac{-1-\sqrt[]{2}}{2}+1).-1](/latexrender/pictures/40b79e5ea0fe0a0f65d3a669fcaf6059.png)
![y = (\frac{1-\sqrt[]{2}}{2}).-1 y = (\frac{1-\sqrt[]{2}}{2}).-1](/latexrender/pictures/0813092c5a6ce42ad8471ca83bf06de3.png)
![y = -\frac{1-\sqrt[]{2}}{2} y = -\frac{1-\sqrt[]{2}}{2}](/latexrender/pictures/21e6ba22541f13eb3b5a99ae9e962c69.png)
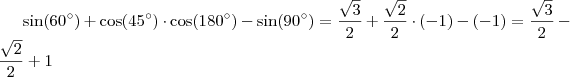
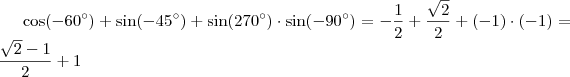


![sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.(-1)-(-1)=\frac{\sqrt[]{3}}{2}-\frac{\sqrt[]{2}}{2}+1 sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.(-1)-(-1)=\frac{\sqrt[]{3}}{2}-\frac{\sqrt[]{2}}{2}+1](/latexrender/pictures/66dab0eb2f0c045e17554ac45d6b205b.png)
![sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.(-1)-(1)=\frac{\sqrt[]{3}}{2}-\frac{\sqrt[]{2}}{2}+1 sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.(-1)-(1)=\frac{\sqrt[]{3}}{2}-\frac{\sqrt[]{2}}{2}+1](/latexrender/pictures/9cc89cfd794575b103d100444c84f588.png)
 Logo:
Logo: ![[tex]sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.0=0 [tex]sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.0=0](/latexrender/pictures/1cd4fd697722946fc8746e913e9ee3f4.png)

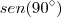 por -1. Mesmo assim, a resposta fica:
por -1. Mesmo assim, a resposta fica: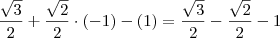
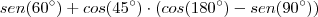
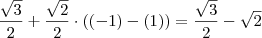
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)