 por JustForFun » Dom Nov 07, 2010 01:23
por JustForFun » Dom Nov 07, 2010 01:23
Olá pessoal, td bem?
Estou estudando pra uma prova e um dos assuntos será trigonometria, tenho que treinar muito!
Gostaria que alguém conferisse se resolvi o seguinte exercício corretamente e se dá pra simplificar mais ainda a resposta final.
(Agora com o editor de fórumla

)
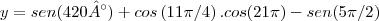
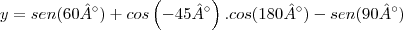
![y= \frac{\sqrt[]{3}}{2}+\left(-\frac{\sqrt[]{2}}{2} \right) . [-1 -1] y= \frac{\sqrt[]{3}}{2}+\left(-\frac{\sqrt[]{2}}{2} \right) . [-1 -1]](/latexrender/pictures/0166dfa8c49bc08296a3f627e162f491.png)
![y= \frac{\sqrt[]{3}-\sqrt[]{2}}{2} . \left(-2 \right) y= \frac{\sqrt[]{3}-\sqrt[]{2}}{2} . \left(-2 \right)](/latexrender/pictures/6fc6cd5d48e3457ebfbeb0d3d28981da.png)
![y= \frac{-2\left(\sqrt[]{3}-\sqrt[]{2} \right)}{2} y= \frac{-2\left(\sqrt[]{3}-\sqrt[]{2} \right)}{2}](/latexrender/pictures/eeaea8ef27f8875a206faf4a9d8c45ab.png)
E aí tudo certinho? Será que agora posso cortar o 2 de cima com o de baixo? Aí vai ficar -raiz de 3 + raiz de 2?
Vlw!!
-
JustForFun
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Nov 05, 2010 22:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por JustForFun » Dom Nov 07, 2010 01:33
por JustForFun » Dom Nov 07, 2010 01:33
-
JustForFun
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Nov 05, 2010 22:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por JustForFun » Seg Nov 08, 2010 20:37
por JustForFun » Seg Nov 08, 2010 20:37
Ninguém?

-
JustForFun
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Nov 05, 2010 22:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por JustForFun » Ter Nov 09, 2010 15:48
por JustForFun » Ter Nov 09, 2010 15:48
Olá Fantini! Obrigado pela resposta

Acho que você se equivocou
![sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.(-1)-(-1)=\frac{\sqrt[]{3}}{2}-\frac{\sqrt[]{2}}{2}+1 sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.(-1)-(-1)=\frac{\sqrt[]{3}}{2}-\frac{\sqrt[]{2}}{2}+1](/latexrender/pictures/66dab0eb2f0c045e17554ac45d6b205b.png)
Deveria ser:
![sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.(-1)-(1)=\frac{\sqrt[]{3}}{2}-\frac{\sqrt[]{2}}{2}+1 sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.(-1)-(1)=\frac{\sqrt[]{3}}{2}-\frac{\sqrt[]{2}}{2}+1](/latexrender/pictures/9cc89cfd794575b103d100444c84f588.png)
Seno 90° = 1 e não -1
Mesmo aplicando o -1 ali, acho que você se confundiu nas contas, pois:

Logo:
![[tex]sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.0=0 [tex]sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.0=0](/latexrender/pictures/1cd4fd697722946fc8746e913e9ee3f4.png)
Se alguém puder esclarecer, agradeço

-
JustForFun
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Nov 05, 2010 22:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Ter Nov 09, 2010 21:19
por MarceloFantini » Ter Nov 09, 2010 21:19
Realmente, troquei sem querer o
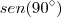
por -1. Mesmo assim, a resposta fica:
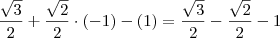
A menos que você esteja errando toda vez ao digitar e a equação verdadeira seja:
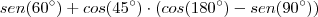
Que em tal caso fica:
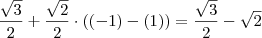
Se o caso for o segundo, realmente eu errei nas contas duplamente (ao confundir o valor do seno e ao fazer a multiplicação), caso contrário, apenas errei um sinal.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [trigonometria] trigonometria em triangulo qualquer
por biamassa00 » Sex Mai 25, 2012 22:19
- 0 Respostas
- 3589 Exibições
- Última mensagem por biamassa00

Sex Mai 25, 2012 22:19
Trigonometria
-
- (Trigonometria) problema trigonometria
por Luizap11 » Qui Dez 05, 2013 00:33
- 2 Respostas
- 5264 Exibições
- Última mensagem por Edunclec

Qui Dez 05, 2013 20:53
Trigonometria
-
- trigonometria
por Cleyson007 » Qua Set 24, 2008 19:44
- 2 Respostas
- 3412 Exibições
- Última mensagem por admin

Ter Set 30, 2008 19:08
Trigonometria
-
- trigonometria
por Micheline » Dom Jan 25, 2009 16:21
- 5 Respostas
- 4956 Exibições
- Última mensagem por Cleyson007

Seg Jan 26, 2009 17:27
Trigonometria
-
- Trigonometria
por Flavio » Sex Fev 13, 2009 21:29
- 5 Respostas
- 5114 Exibições
- Última mensagem por Molina

Seg Fev 16, 2009 01:53
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![y= \frac{\sqrt[]{3}}{2}+\left(-\frac{\sqrt[]{2}}{2} \right) . [-1 -1] y= \frac{\sqrt[]{3}}{2}+\left(-\frac{\sqrt[]{2}}{2} \right) . [-1 -1]](/latexrender/pictures/0166dfa8c49bc08296a3f627e162f491.png)
![y= \frac{\sqrt[]{3}-\sqrt[]{2}}{2} . \left(-2 \right) y= \frac{\sqrt[]{3}-\sqrt[]{2}}{2} . \left(-2 \right)](/latexrender/pictures/6fc6cd5d48e3457ebfbeb0d3d28981da.png)
![y= \frac{-2\left(\sqrt[]{3}-\sqrt[]{2} \right)}{2} y= \frac{-2\left(\sqrt[]{3}-\sqrt[]{2} \right)}{2}](/latexrender/pictures/eeaea8ef27f8875a206faf4a9d8c45ab.png)


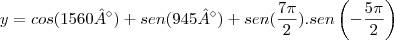
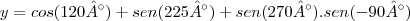
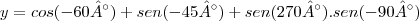
![y = -\frac{1}{2}+\left(-\frac{\sqrt[]{2}}{2} \right)-1.(-1) y = -\frac{1}{2}+\left(-\frac{\sqrt[]{2}}{2} \right)-1.(-1)](/latexrender/pictures/9c19f076ecc190b1de48880027f568dc.png)
![y = (\frac{-1-\sqrt[]{2}}{2}+1).-1 y = (\frac{-1-\sqrt[]{2}}{2}+1).-1](/latexrender/pictures/40b79e5ea0fe0a0f65d3a669fcaf6059.png)
![y = (\frac{1-\sqrt[]{2}}{2}).-1 y = (\frac{1-\sqrt[]{2}}{2}).-1](/latexrender/pictures/0813092c5a6ce42ad8471ca83bf06de3.png)
![y = -\frac{1-\sqrt[]{2}}{2} y = -\frac{1-\sqrt[]{2}}{2}](/latexrender/pictures/21e6ba22541f13eb3b5a99ae9e962c69.png)
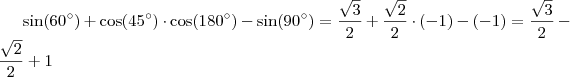
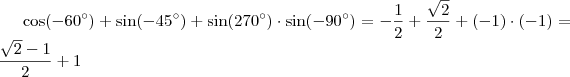


![sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.(-1)-(-1)=\frac{\sqrt[]{3}}{2}-\frac{\sqrt[]{2}}{2}+1 sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.(-1)-(-1)=\frac{\sqrt[]{3}}{2}-\frac{\sqrt[]{2}}{2}+1](/latexrender/pictures/66dab0eb2f0c045e17554ac45d6b205b.png)
![sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.(-1)-(1)=\frac{\sqrt[]{3}}{2}-\frac{\sqrt[]{2}}{2}+1 sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.(-1)-(1)=\frac{\sqrt[]{3}}{2}-\frac{\sqrt[]{2}}{2}+1](/latexrender/pictures/9cc89cfd794575b103d100444c84f588.png)
 Logo:
Logo: ![[tex]sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.0=0 [tex]sen(60)+cos(45).cos(180)-sen(90)=\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{2}}{2}.0=0](/latexrender/pictures/1cd4fd697722946fc8746e913e9ee3f4.png)

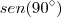 por -1. Mesmo assim, a resposta fica:
por -1. Mesmo assim, a resposta fica: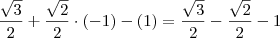
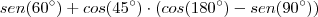
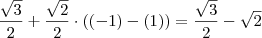


 , avisa que eu resolvo.
, avisa que eu resolvo.

