Enunciado: Expresse a quantidade dada como um único logaritmo
37) ln 5 + 5 ln 3=> (tentei resolver assim)
ln 5 + ln
 => ln 5 *
=> ln 5 *  => ln 5 * 243 => ln 1215
=> ln 5 * 243 => ln 1215(confere com a resposta atrás do livro, acho que tá certo)
38) ln (a+b)+ln (a-b)-2ln c => ln (a+b)*(a-c)-ln
 =
==ln

(essa eu não sei se está certa ou não, pq atras do livro não tem a resposta dela)
39)ln(1+x²)+
 ln x - ln sen x =
ln x - ln sen x == ln
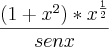 =>
=> ![\frac{(1+{x}^{2})* \sqrt[2]{x}}}{sen x} \frac{(1+{x}^{2})* \sqrt[2]{x}}}{sen x}](/latexrender/pictures/08401550bb87dd2b33ee1c4faab6cb05.png)
(a resposta dessa tbm confere com a resposta do livro)
Enunciado: Resolva cada equação em x.
[desse tipo eu não sei resolver muito bem, por isso gostaria de uma explicação pausada de como resolvê-las]

47) a) 2 ln x = 1
= ln x² = 1
= x² = ln 1
= x=
![\sqrt[]{ln 1} \sqrt[]{ln 1}](/latexrender/pictures/abc4be5793b5903c3aa34370ce8d2d09.png) => (não sei o resto
=> (não sei o resto  )
)b)
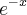 =5
=5(essa eu nn sei nein por onde começar
49) a)
 =3
=3(pelo visto também é para aplicar o logaritmo natural, mas não sei como fazê-lo =[ )
b) ln x + ln (x-1) =1
= ln x (x-1) =1
= ln x²-x =1
= e¹=x²-x
Por favor pessoal, preciso aprender isso urgentemente! me ajuudeem
coloquem a explicação, por gentiliza. Deus abençoe
Ps.: Os exercicios são da seção 1.6 do livro Cálculo 1 de James Stewart



 . Lembrando agora que isto significa que
. Lembrando agora que isto significa que  , teremos duas possíveis respostas:
, teremos duas possíveis respostas:  e
e 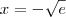 . Pela definição de logaritmo, precisamos que ele seja positivo, logo
. Pela definição de logaritmo, precisamos que ele seja positivo, logo 

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.