 por aninha1701 » Qui Mar 12, 2009 11:56
por aninha1701 » Qui Mar 12, 2009 11:56
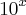
=4
alternativas:
a)2
b)2.log²
c)log²
d)log de 10 na base 4
e)0
-
aninha1701
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Mar 12, 2009 11:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em ciencias biologicas
- Andamento: cursando
 por Marcampucio » Qui Mar 12, 2009 12:42
por Marcampucio » Qui Mar 12, 2009 12:42
Acho que a alternativa d) está invertida. Não seria

?
tome logarítimos dos dois lados (escolhi a base 10):
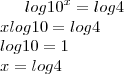
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por Molina » Qui Mar 12, 2009 17:38
por Molina » Qui Mar 12, 2009 17:38
Boa tarde, Aninha.
Acho que as possíveis soluções que você postou há algum engano, pois realmente, da forma que está nenhuma delas satisfaz

.
Como foi muito bem observado pelo nosso amigo, podemos utilizar o log para esta questão, ficando

.
Ou a resposta é a letra d) pelo motivo já exposto acima ou então é a letra b), pois acho que você deve ter se confundido, querendo colocar
 (lê-se duas vezes o log de 2 na base 10)
(lê-se duas vezes o log de 2 na base 10).
Pois note que

Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Qual o valor de x na equação
por Killder » Ter Nov 27, 2012 09:40
- 4 Respostas
- 3593 Exibições
- Última mensagem por Killder

Qua Nov 28, 2012 00:43
Álgebra Elementar
-
- Qual o valor de K?
por Talvane Ramos » Ter Mar 23, 2010 13:12
- 2 Respostas
- 4482 Exibições
- Última mensagem por joao_pimentel

Qua Dez 14, 2011 20:21
Sistemas de Equações
-
- Qual o valor de (-1)^2/6?
por Abelardo » Ter Abr 12, 2011 23:55
- 28 Respostas
- 15520 Exibições
- Última mensagem por MarceloFantini

Ter Fev 14, 2012 16:26
Álgebra Elementar
-
- Qual é o valor de m
por andersontricordiano » Ter Mai 10, 2011 21:58
- 2 Respostas
- 1993 Exibições
- Última mensagem por DanielRJ

Ter Mai 10, 2011 22:32
Funções
-
- Limite-Qual o Valor de a?
por Luthius » Sex Jul 31, 2009 11:19
- 13 Respostas
- 11525 Exibições
- Última mensagem por Elcioschin

Seg Ago 03, 2009 19:02
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
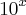 =4
=4
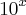 =4
=4
 ?
?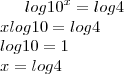

 .
. .
. (lê-se duas vezes o log de 2 na base 10).
(lê-se duas vezes o log de 2 na base 10).


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
