logaritmos em função de a e b

[crfsatisfaction]

Se log34=a e log45=b , então o valor de log35 em função de a e b é:
a)1/a+b b)b/a c)1/a.b d)a/b e)a.b
só encontrei exemplos com multiplicaçao:log2=a,log3=b,o valor de log180 é: dai fiz log(2.3.3.10)
log2+log3+log3+log10
E cheguei a esse resultado a+2b+1 mas no caso do exercicio acima nao consegui utilizar esse mesmo metodo,talvez se usase log34+1 e depois passase para a multiplicaçao mas não sei se é possivel,por favor me deem uma força nesta resoluçao,desde ja agradeço

[Molina]

Boa noite.

Você está usando a propriedade errada. Lembre-se da propriedade de mudança de base:



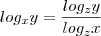
Trazendo esta propriedade para o seu problema, temos que:




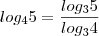
Consegue resolver agora?