 por 0 kelvin » Dom Dez 12, 2010 13:08
por 0 kelvin » Dom Dez 12, 2010 13:08
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Lógica Digital] Sistema Numérico Conversão Base X - Base 10
por Luc4sPaulo » Sex Fev 17, 2017 12:32
- 0 Respostas
- 4165 Exibições
- Última mensagem por Luc4sPaulo

Sex Fev 17, 2017 12:32
Lógica
-
- [Base] Encontrar uma base e a dimensão do subespaço
por anderson_wallace » Sex Jan 10, 2014 00:48
- 3 Respostas
- 13858 Exibições
- Última mensagem por Guilherme Pimentel

Qua Jan 15, 2014 05:23
Álgebra Linear
-
- [Mudança de Base] Matriz de mudança de base ? para ?.
por fabriel » Ter Nov 26, 2013 15:38
- 0 Respostas
- 2104 Exibições
- Última mensagem por fabriel

Ter Nov 26, 2013 15:38
Álgebra Linear
-
- N.C na forma trigonométrica
por geriane » Seg Jul 05, 2010 13:45
- 2 Respostas
- 2696 Exibições
- Última mensagem por geriane

Seg Jul 05, 2010 14:23
Números Complexos
-
- MMC e MDC forma fatorada
por gusousa » Dom Mai 04, 2014 20:25
- 1 Respostas
- 2130 Exibições
- Última mensagem por alienante

Seg Mai 05, 2014 12:15
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![\log_2{3} + \log_2{\sqrt[2]{3}} \log_2{3} + \log_2{\sqrt[2]{3}}](/latexrender/pictures/32e7afb524d1ecaeda3e71b9c66713ae.png)
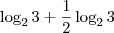
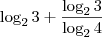
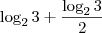
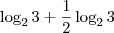
 então o y pode "passar" para uma raiz enésima no logaritmando?
então o y pode "passar" para uma raiz enésima no logaritmando?


![\log_2{3} + \log_2{\sqrt[2]{3}} \log_2{3} + \log_2{\sqrt[2]{3}}](/latexrender/pictures/32e7afb524d1ecaeda3e71b9c66713ae.png)
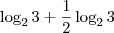
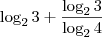
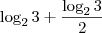
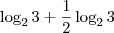
 então o y pode "passar" para uma raiz enésima no logaritmando?
então o y pode "passar" para uma raiz enésima no logaritmando?

