-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478190 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 531992 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 495511 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 706221 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2122486 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por manuoliveira » Qui Set 30, 2010 23:34
por manuoliveira » Qui Set 30, 2010 23:34
Não estou conseguindo resolver a seguinte questão, agradeço desde já puder ajudar!
1) Sejam x e y números reais satisfazendo as equações
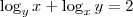
e x²y + y² = 12x. Determine o valor do produto x.y.
Resposta: 09
-
manuoliveira
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por Elcioschin » Sex Out 01, 2010 18:01
por Elcioschin » Sex Out 01, 2010 18:01
log[y](x) + log[x](y) = 2 -----> Condições de existência x > 0, y > 0 , x ><1 , y >< 1
log[y](x) + 1/log[y](x) = 2
{log[y](x)}² - 2*log[x](y) + 1 = 0 ----> Equação do 2º grau ----> Raiz dupla: log[y](x) = 1 ----> x = y
x²y + y² = 12x -----> x²*x + y² = 12x -----> x³ + x² = 12x ----> Dividindo por x ----> x² + x - 12 = 0 ----> Equação do 2º grau
Raízes ----> x = - 4 (não serve) e x = +3 ----> y = +3 -----> x*y = 9
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por jefferson0209 » Ter Set 22, 2015 18:38
por jefferson0209 » Ter Set 22, 2015 18:38
alguem me ajuda?
1)sendo log2=u e log3=v,determine:
a)log12
b)log15
2)calcula:
log 81+ log625-log100
.. 3 . . 5
-
jefferson0209
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Ter Set 22, 2015 15:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: matematica
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Logaritmos] Dúvida em um exercicio envolvendo logaritmos.
por LuizGustavo » Sex Jun 01, 2012 22:48
- 2 Respostas
- 4456 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:38
Logaritmos
-
- [Logaritmos] equação com logaritmos
por natanaelvoss » Sex Dez 07, 2012 20:25
- 2 Respostas
- 6094 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:40
Logaritmos
-
- logaritmos
por celisecorrea » Ter Set 30, 2008 17:17
- 2 Respostas
- 2750 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:38
Logaritmos
-
- LOGARITMOS
por DESESPERADA » Qua Dez 30, 2009 13:25
- 2 Respostas
- 2648 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:37
Matemática Financeira
-
- Logaritmos
por cristina » Qua Jun 02, 2010 10:07
- 1 Respostas
- 2054 Exibições
- Última mensagem por Cleyson007

Qua Jun 02, 2010 13:30
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
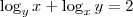 e x²y + y² = 12x. Determine o valor do produto x.y.
e x²y + y² = 12x. Determine o valor do produto x.y.
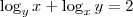 e x²y + y² = 12x. Determine o valor do produto x.y.
e x²y + y² = 12x. Determine o valor do produto x.y.

