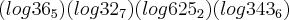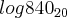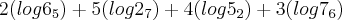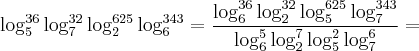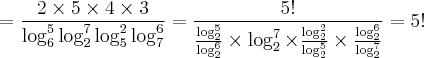por kalanicastanho » Seg Mai 30, 2016 09:30
por kalanicastanho » Seg Mai 30, 2016 09:30
.Olá gostaria de pedir ajuda para resolver um exercício de expressão logaritima da prova do processo seletivo do IFRS
É a seguinte questão
O valor da expressão
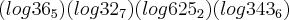
a)log
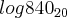
b)42
c)5! RESPOSTA GABARITO
d)
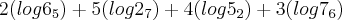
e)55
Comecei resolvendo o primeiro logaritmo porém no começo já dificultou tentei aplicar a propriedade de potência mas mesmo assim ficou ruim pra resolver, alguem poderia dizer se é necessário ou se deve e pode mudar todos logaritmos pra mesma base?
-
kalanicastanho
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Mai 30, 2016 09:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por nakagumahissao » Seg Mai 30, 2016 23:10
por nakagumahissao » Seg Mai 30, 2016 23:10
Sim, você pode mudar de base. Ficaria muito mais facil trabalhar com esses logaritmos.
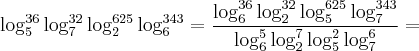
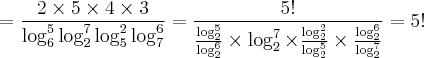
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação logaritima
por Maria Tamires » Sex Jul 12, 2013 11:52
- 1 Respostas
- 1281 Exibições
- Última mensagem por young_jedi

Sex Jul 12, 2013 19:53
Logaritmos
-
- Duvida em expressão
por ginrj » Sex Mar 06, 2009 18:45
- 2 Respostas
- 4215 Exibições
- Última mensagem por ginrj

Sáb Mar 07, 2009 12:01
Álgebra Elementar
-
- Expressão duvida !!!
por LuizCarlos » Qui Ago 11, 2011 14:57
- 1 Respostas
- 1637 Exibições
- Última mensagem por Molina

Qui Ago 11, 2011 16:40
Álgebra Elementar
-
- Dúvida em expressão
por Danilo » Ter Ago 14, 2012 00:52
- 3 Respostas
- 1793 Exibições
- Última mensagem por MarceloFantini

Ter Ago 14, 2012 01:30
Álgebra Elementar
-
- Dúvida sobre ''sinal da expressão ax+b''
por Danilo » Dom Abr 22, 2012 03:41
- 5 Respostas
- 2953 Exibições
- Última mensagem por DanielFerreira

Ter Abr 24, 2012 20:20
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.