 por SCHOOLGIRL+T » Qui Nov 15, 2012 12:02
por SCHOOLGIRL+T » Qui Nov 15, 2012 12:02
-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Qui Nov 15, 2012 13:15
por DanielFerreira » Qui Nov 15, 2012 13:15
danjr5 escreveu:Uma
inequação fracionária não pode ser resolvida dessa forma. Deve-se levar em consideração o
denominador, também.
Tentarei explicar com um simples exemplo, veja:
Resolva
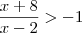
- Inicialmente, devemos fazer com que depois do símbolo de maior (ou qualquer outro) seja zero, ou seja;
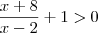
- Devemos tirar o MMC;
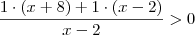
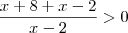

- Devemos estudar o sinal do numerador e do denominador;
Numerador:
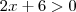

Denominador:
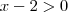

- Quadro de sinais
___-____(- 3)
____+______________+___________-____________-_____(+ 2)
_____+___________+____(- 3)____-_____(+ 2)
_____+________ Daí,

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por SCHOOLGIRL+T » Qui Nov 15, 2012 13:59
por SCHOOLGIRL+T » Qui Nov 15, 2012 13:59
danjr5 escreveu:danjr5 escreveu:Uma
inequação fracionária não pode ser resolvida dessa forma. Deve-se levar em consideração o
denominador, também.
Tentarei explicar com um simples exemplo, veja:
Resolva
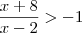
- Inicialmente, devemos fazer com que depois do símbolo de maior (ou qualquer outro) seja zero, ou seja;
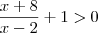
- Devemos tirar o MMC;
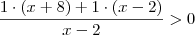
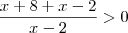

- Devemos estudar o sinal do numerador e do denominador;
Numerador:
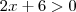

Denominador:
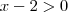

- Quadro de sinais
___-____(- 3)
____+______________+___________-____________-_____(+ 2)
_____+___________+____(- 3)____-_____(+ 2)
_____+________ Daí,

Fiz como vc disse e encontrei:
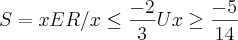
Está correto?
-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Qui Nov 15, 2012 14:23
por DanielFerreira » Qui Nov 15, 2012 14:23
Sim!
Mas, tem um detalhe, o denominador não pode ter

. Pois, seria IMPOSSÍVEL, enfim o denominador seria ZERO.
O correto seria
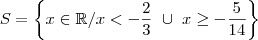
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por SCHOOLGIRL+T » Qui Nov 15, 2012 14:30
por SCHOOLGIRL+T » Qui Nov 15, 2012 14:30
danjr5 escreveu:Sim!
Mas, tem um detalhe, o denominador não pode ter

. Pois, seria IMPOSSÍVEL, enfim o denominador seria ZERO.
O correto seria
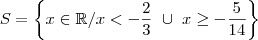
Ops, me esqueci deste detalhe. Mto obrigada^^
-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Qui Nov 15, 2012 14:48
por DanielFerreira » Qui Nov 15, 2012 14:48
Não há de quê!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2571 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1849 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
-
- Logaritmo
por JailsonJr » Sex Mai 21, 2010 05:11
- 3 Respostas
- 2733 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:33
Logaritmos
-
- Logaritmo (UF-CE)
por JailsonJr » Sáb Mai 22, 2010 04:56
- 6 Respostas
- 5270 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:32
Logaritmos
-
- Logaritmo
por nan_henrique » Sex Jul 09, 2010 18:38
- 1 Respostas
- 2279 Exibições
- Última mensagem por Elcioschin

Sex Jul 09, 2010 19:42
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


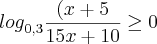
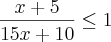


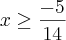


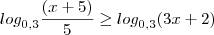

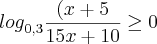
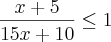


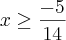


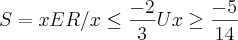

 . Pois, seria IMPOSSÍVEL, enfim o denominador seria ZERO.
. Pois, seria IMPOSSÍVEL, enfim o denominador seria ZERO.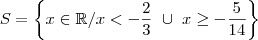

. Pois, seria IMPOSSÍVEL, enfim o denominador seria ZERO.



 .
.



