 por natanskt » Sáb Out 09, 2010 13:31
por natanskt » Sáb Out 09, 2010 13:31
quais as raizes reais da equação

não consigo intender nada dessa resolução,alguem pode me explicar detalhadamente?
só essa parte que eu não intendo,
não foi eu que fiz essa resoluçao peguei um pedação da apostila,só que eu não intendo
primeiro fiz uma mudança de base:
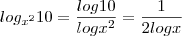
daonde saiu esse 2+...?
e para economizar na escrita tomamos
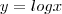
ficando com:

-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por DanielRJ » Sáb Out 09, 2010 13:42
por DanielRJ » Sáb Out 09, 2010 13:42
natanskt escreveu:quais as raizes reais da equação

não consigo intender nada dessa resolução,alguem pode me explicar detalhadamente?
só essa parte que eu não intendo,
não foi eu que fiz essa resoluçao peguei um pedação da apostila,só que eu não intendo
primeiro fiz uma mudança de base:
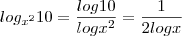
daonde saiu esse 2+...?
e para economizar na escrita tomamos
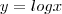
ficando com:

Ele usou a propriedade do logaritmos. o logaritmano elevado a um numero pode passar multiplicando o logaritmo assim:
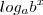
------>>>>
 Natan entra ai no msn pra gente conversar te espero flw!
Natan entra ai no msn pra gente conversar te espero flw!
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação logaritmica
por DanielRJ » Qui Out 07, 2010 17:20
- 4 Respostas
- 2459 Exibições
- Última mensagem por DanielRJ

Sáb Out 09, 2010 15:28
Logaritmos
-
- (AFA) equação logaritmica
por natanskt » Sex Out 08, 2010 12:27
- 2 Respostas
- 1871 Exibições
- Última mensagem por Molina

Sex Out 08, 2010 14:30
Funções
-
- (AFA) equação logaritmica
por natanskt » Sex Out 08, 2010 12:30
- 1 Respostas
- 1455 Exibições
- Última mensagem por DanielRJ

Sex Out 08, 2010 14:13
Funções
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 14:51
- 2 Respostas
- 1821 Exibições
- Última mensagem por natanskt

Seg Out 11, 2010 15:58
Logaritmos
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 15:00
- 1 Respostas
- 1638 Exibições
- Última mensagem por Douglasm

Sáb Out 09, 2010 17:29
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

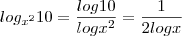 daonde saiu esse 2+...?
daonde saiu esse 2+...?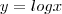 ficando com:
ficando com:


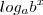 ------>>>>
------>>>>
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.