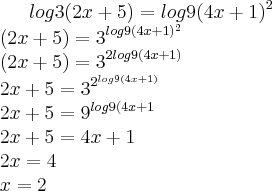Está incorreto. Vou primeiramente corrigir a primeira parte da tua resolução e posteriormente apresentar duas formas que eu considero mais simples de fazer.
Correção:
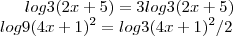
Nessa parte tu separou os dois lados da equação para "transforma-los" em algo mais adequado (o que pode ser feito sem problemas), porem a primeira ficou errada. Perceba que tu escreveu

, ou seja, tu disse que o log3(2x+5) é o mesmo que tres vezes ele (3log3(2x+5)). A outra transformação, no entanto, esta sim correta
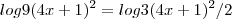
Resolução (1ª forma): Esta é bem semlhante ao que tu fez. Utilizamos a propriedade de mudança de base de logaritmos.
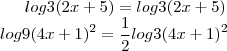
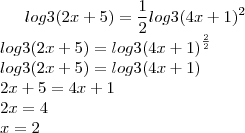
Perceba que o

que estava na frente do log, passou a ser expoente do logaritmando, esta é uma das propriedades de logaritmos. Essa operação deve ser feita antes de cancelarmos os log's.
Resolução (2ª forma): Nesta forma vamos resolver sem fazer a troca de base, apenas resolvendo logaritmo pela definição.
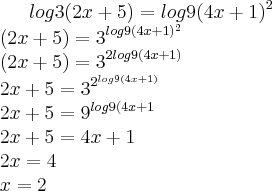
Perceba que foi utilizada uma propriedade de exponenciais:

Como podemos ver, novamente utilizamos a propriedade para mover o expoente do logaritmando para frente do log.
É importante sempre ter a mão uma folha com as propriedades de logaritmos (e exponenciais) caso ainda não estejam tão fixadas.
Caso algo ainda continue confuso, pode mandar uma msg que eu respondo.


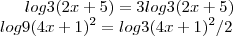
 , ou seja, tu disse que o log3(2x+5) é o mesmo que tres vezes ele (3log3(2x+5)). A outra transformação, no entanto, esta sim correta
, ou seja, tu disse que o log3(2x+5) é o mesmo que tres vezes ele (3log3(2x+5)). A outra transformação, no entanto, esta sim correta 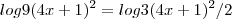
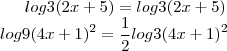
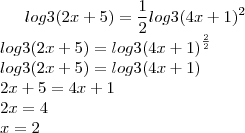
 que estava na frente do log, passou a ser expoente do logaritmando, esta é uma das propriedades de logaritmos. Essa operação deve ser feita antes de cancelarmos os log's.
que estava na frente do log, passou a ser expoente do logaritmando, esta é uma das propriedades de logaritmos. Essa operação deve ser feita antes de cancelarmos os log's.