 por apotema2010 » Seg Mar 08, 2010 11:21
por apotema2010 » Seg Mar 08, 2010 11:21
Sabendo-se que log2=m, o valor de
![{log} _ {4} \sqrt [3] {25} {log} _ {4} \sqrt [3] {25}](/latexrender/pictures/4e752cf30b29b4d24b1a4cfb633b7691.png)
, resolvi da seguinte forma e não deu certo:
![{log} _ {4} \sqrt [3] {25} {log} _ {4} \sqrt [3] {25}](/latexrender/pictures/4e752cf30b29b4d24b1a4cfb633b7691.png)
=x

x=2/3
não é essa a resposta.
-
apotema2010
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qua Fev 17, 2010 14:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por apotema2010 » Ter Mar 09, 2010 10:27
por apotema2010 » Ter Mar 09, 2010 10:27
Olha as alternativas que tenho:
a)
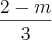
b)

c)
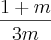
d)
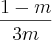
e)
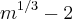
-
apotema2010
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qua Fev 17, 2010 14:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por MarceloFantini » Ter Mar 09, 2010 19:23
por MarceloFantini » Ter Mar 09, 2010 19:23
Vou continuar o raciocínio e você perceberá. Vou multiplicar a segunda fração em cima e embaixo por

:
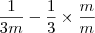
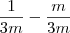
Mesmo denominador, posso deixar tudo em uma fração:

Resposta letra D.
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Logaritmo de base E
por Moreno1986 » Sex Ago 13, 2010 14:41
- 0 Respostas
- 726 Exibições
- Última mensagem por Moreno1986

Sex Ago 13, 2010 14:41
Logaritmos
-
- Logaritmo: determinar a base
por _Liilo » Dom Out 31, 2010 19:43
- 2 Respostas
- 5588 Exibições
- Última mensagem por _Liilo

Dom Out 31, 2010 22:12
Logaritmos
-
- Logaritmo que base e logaritmando não são divisiveis iguais
por Linuxmh » Qua Jul 17, 2013 20:15
- 4 Respostas
- 3498 Exibições
- Última mensagem por Linuxmh

Sex Jul 19, 2013 12:01
Logaritmos
-
- [Volumes de sólidos por rotação] Volume mudando os eixos
por Edmond Dantes » Sáb Out 20, 2018 11:31
- 2 Respostas
- 5873 Exibições
- Última mensagem por Edmond Dantes

Sáb Out 20, 2018 16:40
Cálculo: Limites, Derivadas e Integrais
-
- [Lógica Digital] Sistema Numérico Conversão Base X - Base 10
por Luc4sPaulo » Sex Fev 17, 2017 12:32
- 0 Respostas
- 4158 Exibições
- Última mensagem por Luc4sPaulo

Sex Fev 17, 2017 12:32
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{log} _ {4} \sqrt [3] {25} {log} _ {4} \sqrt [3] {25}](/latexrender/pictures/4e752cf30b29b4d24b1a4cfb633b7691.png) , resolvi da seguinte forma e não deu certo:
, resolvi da seguinte forma e não deu certo:![{log} _ {4} \sqrt [3] {25} {log} _ {4} \sqrt [3] {25}](/latexrender/pictures/4e752cf30b29b4d24b1a4cfb633b7691.png) =x
=x

![{log} _ {4} \sqrt [3] {25} {log} _ {4} \sqrt [3] {25}](/latexrender/pictures/4e752cf30b29b4d24b1a4cfb633b7691.png) , resolvi da seguinte forma e não deu certo:
, resolvi da seguinte forma e não deu certo:![{log} _ {4} \sqrt [3] {25} {log} _ {4} \sqrt [3] {25}](/latexrender/pictures/4e752cf30b29b4d24b1a4cfb633b7691.png) =x
=x

![\log_{4} \sqrt[3]{5^2} = \frac {\log {5^ {\frac {2} {3} } } } {\log {2^2}} \log_{4} \sqrt[3]{5^2} = \frac {\log {5^ {\frac {2} {3} } } } {\log {2^2}}](/latexrender/pictures/aa2407f3ad9e40d5f35bc13633dbb4c3.png)
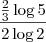
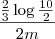


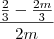
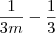


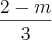

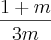
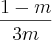
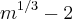

 :
: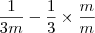
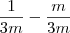



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.