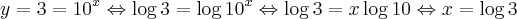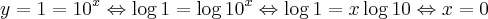por Souo » Ter Jun 30, 2015 01:42
por Souo » Ter Jun 30, 2015 01:42
A soma das raizes da equaç?o
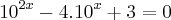
é:
A) 4
B) 1 + log3
C) log2 + log3
D) log5
E) log3
N?o consegui chegar no resultado, alguem pode me ajudar?
-
Souo
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Abr 14, 2015 20:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por nakagumahissao » Qui Jul 02, 2015 10:37
por nakagumahissao » Qui Jul 02, 2015 10:37
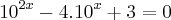
Pelas propriedades da potenciação, podemos reescrever a equação acima da seguinte forma:
[1]
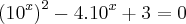
Agora, podemos fazer a seguinte substituição:
[2]

Substituindo [2] em [1], tem-se que:
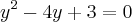
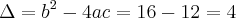
![y = \frac{-b \pm \sqrt[]{\Delta}}{2a} = \frac{4 \pm 2}{2} y = \frac{-b \pm \sqrt[]{\Delta}}{2a} = \frac{4 \pm 2}{2}](/latexrender/pictures/0e20c2db16a4f409f0cf7302b992e0b0.png)

e

Utilizando estes valores obtidos em [1] acima, tem-se que
a) Para y = 3:
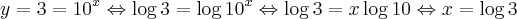
e
b) Para y = 1:
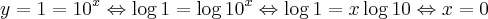
PORTANTO, a soma das raízes da equação dada será: 1 + log(3), ou seja, a resposta é a letra (B)
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por Souo » Qui Jul 02, 2015 22:53
por Souo » Qui Jul 02, 2015 22:53
nakagumahissao escreveu: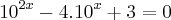
Pelas propriedades da potenciação, podemos reescrever a equação acima da seguinte forma:
[1]
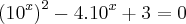
Agora, podemos fazer a seguinte substituição:
[2]

Substituindo [2] em [1], tem-se que:
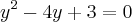
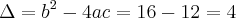
![y = \frac{-b \pm \sqrt[]{\Delta}}{2a} = \frac{4 \pm 2}{2} y = \frac{-b \pm \sqrt[]{\Delta}}{2a} = \frac{4 \pm 2}{2}](/latexrender/pictures/0e20c2db16a4f409f0cf7302b992e0b0.png)

e

Utilizando estes valores obtidos em [1] acima, tem-se que
a) Para y = 3:
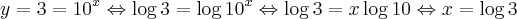
e
b) Para y = 1:
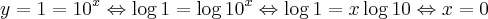
PORTANTO, a soma das raízes da equação dada será: 1 + log(3), ou seja, a resposta é a letra (B)
Entendi, mas o gabarito diz que é a letra E, esta errado?
-
Souo
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Abr 14, 2015 20:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por nakagumahissao » Sex Jul 03, 2015 21:24
por nakagumahissao » Sex Jul 03, 2015 21:24
Desculpe-me, 0 + log 3 = log 3 e a resposta é a letra (e) mesmo
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exponenciais
por Souo » Sáb Jun 20, 2015 14:45
- 1 Respostas
- 1754 Exibições
- Última mensagem por Cleyson007

Dom Jun 21, 2015 09:20
Logaritmos
-
- Exponenciais
por Souo » Qui Jun 18, 2015 19:09
- 1 Respostas
- 1664 Exibições
- Última mensagem por nakagumahissao

Sex Jun 19, 2015 18:50
Logaritmos
-
- Exponenciais
por Souo » Qui Jun 18, 2015 00:20
- 2 Respostas
- 2026 Exibições
- Última mensagem por Souo

Qui Jun 18, 2015 19:04
Logaritmos
-
- Limites exponenciais
por lunayanne » Dom Mar 07, 2010 00:15
- 2 Respostas
- 3350 Exibições
- Última mensagem por lucas92

Ter Abr 13, 2010 03:57
Cálculo: Limites, Derivadas e Integrais
-
- equaçoes exponenciais
por natanskt » Qui Out 07, 2010 13:37
- 7 Respostas
- 4566 Exibições
- Última mensagem por Rogerio Murcila

Qui Out 07, 2010 17:25
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
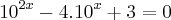 é:
é:
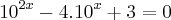 é:
é:
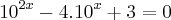
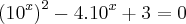

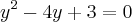
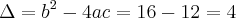
![y = \frac{-b \pm \sqrt[]{\Delta}}{2a} = \frac{4 \pm 2}{2} y = \frac{-b \pm \sqrt[]{\Delta}}{2a} = \frac{4 \pm 2}{2}](/latexrender/pictures/0e20c2db16a4f409f0cf7302b992e0b0.png)