 por adauto martins » Qui Nov 06, 2014 15:46
por adauto martins » Qui Nov 06, 2014 15:46
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por lucassouza » Qui Nov 06, 2014 15:59
por lucassouza » Qui Nov 06, 2014 15:59
Velho, não consegui entender essa resolução =(
-
lucassouza
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Set 15, 2014 15:03
- Formação Escolar: SUPLETIVO
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações Logarítmicas
por Danilo Dias Vilela » Qua Set 01, 2010 11:21
- 1 Respostas
- 1591 Exibições
- Última mensagem por MarceloFantini

Qua Set 01, 2010 21:56
Álgebra Elementar
-
- equações logaritmicas
por vinicius cruz » Dom Mar 06, 2011 19:28
- 3 Respostas
- 2742 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 19:54
Logaritmos
-
- equações logarítmicas
por Luan Cordeiro » Qui Ago 04, 2011 20:42
- 2 Respostas
- 1965 Exibições
- Última mensagem por Claudin

Sex Ago 05, 2011 01:34
Logaritmos
-
- equações logarítmicas
por Luan Cordeiro » Sáb Ago 06, 2011 19:20
- 1 Respostas
- 1500 Exibições
- Última mensagem por LuizAquino

Dom Ago 07, 2011 13:39
Logaritmos
-
- Equações Logarítmicas
 por lucassouza » Qua Nov 05, 2014 17:35
por lucassouza » Qua Nov 05, 2014 17:35
- 1 Respostas
- 1551 Exibições
- Última mensagem por Russman

Qua Nov 05, 2014 23:05
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![\log_{}^{\sqrt[]{x-1}}+\log_{}^{5}=\log_{}^{2x-5} \log_{}^{\sqrt[]{x-1}}+\log_{}^{5}=\log_{}^{2x-5}](/latexrender/pictures/8b30baad37b131d7305a64be366f5668.png) ...
... ...
...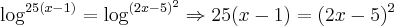 ...
...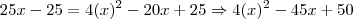


...
...
...


 .
.



