 por Lana Brasil » Seg Jul 21, 2014 22:12
por Lana Brasil » Seg Jul 21, 2014 22:12
Boa Noite.
Comecei a resolver esse exercício e cheguei num sistema, ficou muito grande. Desisti porque achei que fiz errado. Podem me ajudar, por favor? Obrigada pela ajuda!!
Se x e y são números naturais satisfazendo log(8) x + log(4)y² = 6 e log(4)x² + log(8)y = 10, qual o valor de ?xy? (os números entre parêntesis são as bases).
-
Lana Brasil
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Dom Abr 07, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Ter Jul 22, 2014 00:57
por e8group » Ter Jul 22, 2014 00:57
Uma forma ...
Suponha que
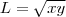
então

.Aplicamos o logaritmo (de base 8) em ambos os membros teremos

.
Agora 'somamos' as equações ...
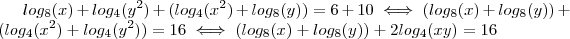
.
Usando (*) e (**) nós temos
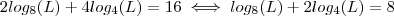
.
Fazendo mudança de base (para 2 ) ...
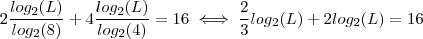
.
Tente avançar
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Pessoa Estranha » Ter Jul 22, 2014 01:10
por Pessoa Estranha » Ter Jul 22, 2014 01:10
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Ter Jul 22, 2014 01:45
por e8group » Ter Jul 22, 2014 01:45
Hahhah sem problemas amigo(a) , isso já aconteceu muito comigo(realmente é difícil apagar dps de tanto esforço p/ redigir) , você que se engana ... (ainda não sou tão rápido no sistema LaTeX) . Não precisa pedir desculpas , novas opiniões , ajudas são sempre bem vindas !! Bem não chequei o resultado , parece que você preferiu encontrar primeiro

...vejamos
Partindo dá última eq. temos

então
![log_2(L)[\frac{1}{3} + 1] =8 log_2(L)[\frac{1}{3} + 1] =8](/latexrender/pictures/befba3c0a81192a150c8f71a8491b0e7.png)
então

e assim
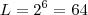
.
Parece que deu certo , ou então nós 2 erramos .
Abraço
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Lana Brasil » Ter Jul 22, 2014 11:48
por Lana Brasil » Ter Jul 22, 2014 11:48
santhiago escreveu:Hahhah sem problemas amigo(a) , isso já aconteceu muito comigo(realmente é difícil apagar dps de tanto esforço p/ redigir) , você que se engana ... (ainda não sou tão rápido no sistema LaTeX) . Não precisa pedir desculpas , novas opiniões , ajudas são sempre bem vindas !! Bem não chequei o resultado , parece que você preferiu encontrar primeiro

...vejamos
Partindo dá última eq. temos

então
![log_2(L)[\frac{1}{3} + 1] =8 log_2(L)[\frac{1}{3} + 1] =8](/latexrender/pictures/befba3c0a81192a150c8f71a8491b0e7.png)
então

e assim
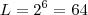
.
Parece que deu certo , ou então nós 2 erramos .
Abraço
Nossa adorei vcs 2!! Obrigada pela grande ajuda e boa vontade. Abraços!!!
-
Lana Brasil
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Dom Abr 07, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Lana Brasil » Ter Jul 22, 2014 11:48
por Lana Brasil » Ter Jul 22, 2014 11:48
Nossa adorei vcs 2!! Obrigada pela grande ajuda e boa vontade. Abraços!!!
-
Lana Brasil
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Dom Abr 07, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Calculo de logaritmo) Encontre o valor de y
por andersontricordiano » Qua Mar 23, 2011 13:39
- 1 Respostas
- 1982 Exibições
- Última mensagem por Molina

Qua Mar 23, 2011 15:07
Logaritmos
-
- [Logaritmo] Como encontrar o valor de x na munheca?
por carvalhothg » Ter Set 13, 2011 15:43
- 6 Respostas
- 3613 Exibições
- Última mensagem por LuizAquino

Qua Set 14, 2011 00:06
Logaritmos
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2567 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1845 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
-
- [Valor de Mercadoria] A partir do valor total de venda
por Gerson Belini » Qua Out 02, 2013 02:17
- 0 Respostas
- 3898 Exibições
- Última mensagem por Gerson Belini

Qua Out 02, 2013 02:17
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


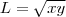 então
então  .Aplicamos o logaritmo (de base 8) em ambos os membros teremos
.Aplicamos o logaritmo (de base 8) em ambos os membros teremos  .
. 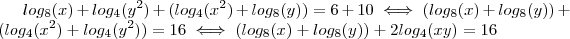 .
.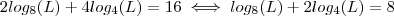 .
. 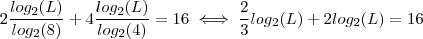 .
. 
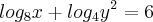

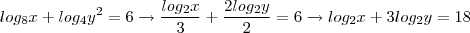
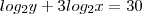

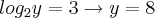
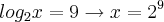
![\sqrt[]{8.{2}^{9}} = \sqrt[]{{2}^{12}} = \sqrt[]{2.2.2.2.2.2.2.2.2.2.2.2} = {2}^{6} = 64 \sqrt[]{8.{2}^{9}} = \sqrt[]{{2}^{12}} = \sqrt[]{2.2.2.2.2.2.2.2.2.2.2.2} = {2}^{6} = 64](/latexrender/pictures/0047172265ca7629fc0c84ed04814e8f.png)

 ...vejamos
...vejamos  então
então ![log_2(L)[\frac{1}{3} + 1] =8 log_2(L)[\frac{1}{3} + 1] =8](/latexrender/pictures/befba3c0a81192a150c8f71a8491b0e7.png) então
então  e assim
e assim 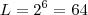 .
. ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.