 por felipemreis » Seg Jan 06, 2014 22:14
por felipemreis » Seg Jan 06, 2014 22:14
Estou com duvida em uma questão de logaritmos, sobre uma equação logarítmica:
Consegui resolver todas as questões menos a
f, tentei resolver usando todas as propriedades dos logaritmos... pensei bastante, mas não consegui chegar a uma resposta com resolução.
No gabarito átras do livro a resposta para a letra
f é:
![S= \left[\left(\frac{1}{256},16 \right) \right] S= \left[\left(\frac{1}{256},16 \right) \right]](/latexrender/pictures/6010589ea115d76141efe9894509cc64.png)
- Anexos
-

-
felipemreis
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Set 13, 2013 13:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por anderson_wallace » Seg Jan 06, 2014 23:07
por anderson_wallace » Seg Jan 06, 2014 23:07
Nesse caso vc pode efetuar uma troca de variável do tipo
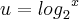
Assim vc vai ficar com a equação
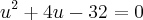
Resolvendo essa equação vc pode encontrar o valor de u e consequentemente de
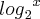
.
-
anderson_wallace
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Seg Dez 30, 2013 17:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ciência e Tecnologia
- Andamento: cursando
 por felipemreis » Ter Jan 07, 2014 15:53
por felipemreis » Ter Jan 07, 2014 15:53
-
felipemreis
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Set 13, 2013 13:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Logaritmo] Resolver equação logaritmica
 por JessicaAraujo » Qui Mai 16, 2013 12:10
por JessicaAraujo » Qui Mai 16, 2013 12:10
- 2 Respostas
- 1510 Exibições
- Última mensagem por JessicaAraujo

Seg Mai 20, 2013 12:09
Funções
-
- [Logaritmo] Função Logarítmica
por Fernando Weber » Seg Fev 25, 2013 22:39
- 3 Respostas
- 2297 Exibições
- Última mensagem por DanielFerreira

Ter Mar 12, 2013 22:53
Logaritmos
-
- Equação logaritmica
por DanielRJ » Qui Out 07, 2010 17:20
- 4 Respostas
- 2465 Exibições
- Última mensagem por DanielRJ

Sáb Out 09, 2010 15:28
Logaritmos
-
- (AFA) equação logaritmica
por natanskt » Sex Out 08, 2010 12:27
- 2 Respostas
- 1873 Exibições
- Última mensagem por Molina

Sex Out 08, 2010 14:30
Funções
-
- (AFA) equação logaritmica
por natanskt » Sex Out 08, 2010 12:30
- 1 Respostas
- 1460 Exibições
- Última mensagem por DanielRJ

Sex Out 08, 2010 14:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![S= \left[\left(\frac{1}{256},16 \right) \right] S= \left[\left(\frac{1}{256},16 \right) \right]](/latexrender/pictures/6010589ea115d76141efe9894509cc64.png)

![S= \left[\left(\frac{1}{256},16 \right) \right] S= \left[\left(\frac{1}{256},16 \right) \right]](/latexrender/pictures/6010589ea115d76141efe9894509cc64.png)

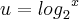
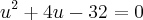
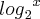 .
.



