 por cleverson » Sáb Nov 30, 2013 13:37
por cleverson » Sáb Nov 30, 2013 13:37
(UEM-PR) Para a funçao de uma variável real definida por f(x)=a log (x-b) ,em que a e b sao números reais, a diferente de 0 e x maior que b, sabe-se que f(3)=0 e f(102)=-6. Sobre o exposto, é correto afirmar que.
A resposta é a+b=-1.
Eu tentei resolver esse exercicio
0=a log (3-b) (base 10)
log 1=a log (3-b) ( cortei os log)
1=a(3-b)
1=3a-ba
3a-ba=1
eu nao sei mais oq fazer a partir daqui se é que esta certo :x
-
cleverson
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Nov 30, 2013 13:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Pessoa Estranha » Sáb Nov 30, 2013 13:57
por Pessoa Estranha » Sáb Nov 30, 2013 13:57
Olá !
Você cometeu eu deslize na seguinte parte:
cleverson escreveu:log 1=a log (3-b) ( cortei os log)
Só podemos "cortar" quando temos algo do tipo:
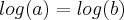
(
na mesma base).
Na parte
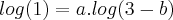
, há uma propriedade para ser aplicada, ficando assim:
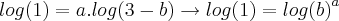
.
Agora sim podemos "cortar" :
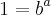
.
Aí, continue o seu raciocínio ....
Espero ter ajudado ....

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Logaritmos] Dúvida em um exercicio envolvendo logaritmos.
por LuizGustavo » Sex Jun 01, 2012 22:48
- 2 Respostas
- 5031 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:38
Logaritmos
-
- [Logaritmos] equação com logaritmos
por natanaelvoss » Sex Dez 07, 2012 20:25
- 2 Respostas
- 6661 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:40
Logaritmos
-
- propriedades de raiz
por theSinister » Ter Jun 21, 2011 22:04
- 10 Respostas
- 6702 Exibições
- Última mensagem por theSinister

Qua Jun 22, 2011 16:16
Álgebra Elementar
-
- propriedades dos radicais
por beatriz gomes » Qua Set 07, 2011 20:11
- 1 Respostas
- 2388 Exibições
- Última mensagem por MarceloFantini

Qua Set 07, 2011 21:02
Álgebra Elementar
-
- Propriedades dos determinates
 por panicox » Sex Set 14, 2018 02:31
por panicox » Sex Set 14, 2018 02:31
- 3 Respostas
- 12580 Exibições
- Última mensagem por Gebe

Sex Set 14, 2018 13:46
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


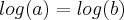 (
(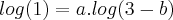 , há uma propriedade para ser aplicada, ficando assim:
, há uma propriedade para ser aplicada, ficando assim: 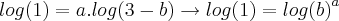 .
. 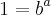 .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.