 . Se a substância apresenta 100.000 átomos desse isótopo no instante t=o, então o número de anos necessários para que o número desses átomos seja igual a 100, admitindo
. Se a substância apresenta 100.000 átomos desse isótopo no instante t=o, então o número de anos necessários para que o número desses átomos seja igual a 100, admitindo 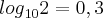 , é?
, é?
 . Se a substância apresenta 100.000 átomos desse isótopo no instante t=o, então o número de anos necessários para que o número desses átomos seja igual a 100, admitindo
. Se a substância apresenta 100.000 átomos desse isótopo no instante t=o, então o número de anos necessários para que o número desses átomos seja igual a 100, admitindo 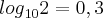 , é?
, é?
 descresce ao passar do tempo , no instante
descresce ao passar do tempo , no instante  teremos
teremos  .
.  unidades de tempo , temos que
unidades de tempo , temos que  . Qual valor que
. Qual valor que  deve assumir para termos
deve assumir para termos  , sabendo que
, sabendo que 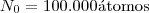 ?
?  . Aplicando logaritmo nos dois lados , vem que
. Aplicando logaritmo nos dois lados , vem que 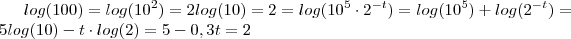 .
. 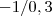 , segue que
, segue que 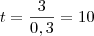 .
.  é medido em unidades 5000 anos , concluímos que
é medido em unidades 5000 anos , concluímos que 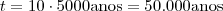 .
.
santhiago escreveu:descresce ao passar do tempo , no instante
teremos
.
Apósunidades de tempo , temos que
. Qual valor que
deve assumir para termos
, sabendo que
?
Basta resolver ,. Aplicando logaritmo nos dois lados , vem que
.
Somando - 5 dos dois lados e após isto mutiplicando ambos lados por, segue que
.
Comoé medido em unidades 5000 anos , concluímos que
.
Comente qualquer dúvida .

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.