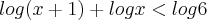
Desde já agradeço.

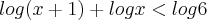

 . Voltando na desigualdade segue que
. Voltando na desigualdade segue que 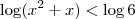 e
e 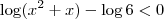 .
. .
. , onde
, onde  e
e 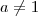 é a base do logaritmo.
é a base do logaritmo.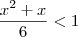 e
e  , de onde
, de onde 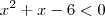 .
.

MarceloFantini escreveu:Bem vinda Thamy. Sobre a questão, usando as propriedades de logaritmo temos que. Voltando na desigualdade segue que
e
.
Novamente usando as propriedades de logaritmo segue que.
Daqui, lembre-se que pela definição de logaritmo isto significa que, onde
e
é a base do logaritmo.
Portantoe
, de onde
.
Agora é só analisar esta desigualdade.



danjr5 escreveu:Thamy,
a equação tem raízes, veja:
Falta estudar o sinal da desigualdade!


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)