 por Deronsi » Sáb Nov 10, 2012 10:05
por Deronsi » Sáb Nov 10, 2012 10:05
eu fiz esse exercício por favor corrija se estiver errado
A população de uma dada região está crescendo exponencialmente. A região tinha 40.000.000 de pessoas em 1980 ( t= 0) e 56.000.000 em 1990. Encontre uma expressão para a população em qualquer instante em t anos. Qual a população prevista para o ano 2000? Qual é o tempo de duplicação ?

-
Deronsi
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Nov 06, 2012 00:10
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: eng. produção
- Andamento: cursando
 por young_jedi » Sáb Nov 10, 2012 14:11
por young_jedi » Sáb Nov 10, 2012 14:11
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Sistemas Lineares: "a, b e c" como "soluções".
por allendy » Qua Set 08, 2010 20:28
- 2 Respostas
- 11303 Exibições
- Última mensagem por allendy

Qua Set 08, 2010 20:37
Sistemas de Equações
-
- [LIMITES] Limite de Raiz "m" de "infinito"
por antonelli2006 » Sáb Set 17, 2011 05:56
- 5 Respostas
- 9192 Exibições
- Última mensagem por LuizAquino

Dom Set 18, 2011 10:08
Cálculo: Limites, Derivadas e Integrais
-
- Matriz constituida de "uns" e "zeros"
por Carolziiinhaaah » Qui Jun 24, 2010 12:08
- 2 Respostas
- 5740 Exibições
- Última mensagem por Carolziiinhaaah

Qui Jun 24, 2010 12:50
Matrizes e Determinantes
-
- Duvida , não consigo prosseguir com o calculo"Help"
por klysman » Ter Mai 01, 2012 20:38
- 5 Respostas
- 2504 Exibições
- Última mensagem por DanielFerreira

Qua Mai 02, 2012 23:10
Geometria Analítica
-
- (ESPCEX)duvida ""besta"'
por natanskt » Sex Nov 26, 2010 17:32
- 3 Respostas
- 4245 Exibições
- Última mensagem por DanielFerreira

Qua Dez 01, 2010 17:07
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





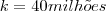



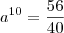
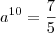
![a=\sqrt[10]{\frac{7}{5}} a=\sqrt[10]{\frac{7}{5}}](/latexrender/pictures/46b9df5e5797c9f04d25745486c2056b.png)
![Q(t)=40.\left(\sqrt[10]{\frac{7}{5}}\right)^t Q(t)=40.\left(\sqrt[10]{\frac{7}{5}}\right)^t](/latexrender/pictures/00ab9b294fe05c5c002352147d0b2dc9.png)
