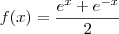 , denominado cosseno hiperbólico é :
, denominado cosseno hiperbólico é :Como eu faço para resolver esse tipo de questão?
Resolvo utilizando logaritmo? E o que é cosseno hiperbólico?

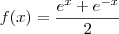 , denominado cosseno hiperbólico é :
, denominado cosseno hiperbólico é :
 e de
e de  são os reais maiores do que 0,
são os reais maiores do que 0,  , e portanto uma função que seja a soma de
, e portanto uma função que seja a soma de  com
com  também é maior do que 0,
também é maior do que 0,  .
. e
e  são inversos um do outro e o menor valor da soma de um número com o seu inverso ocorre quando esse número é igual a 1.
são inversos um do outro e o menor valor da soma de um número com o seu inverso ocorre quando esse número é igual a 1.
fraol escreveu:As imagens dee de
são os reais maiores do que 0,
, e portanto uma função que seja a soma de
com
também é maior do que 0,
.
Para determinar o intervalo real da imagem você precisa determinar qual é o menor valor da função.
Agora, uma dica:e
são inversos um do outro e o menor valor da soma de um número com o seu inverso ocorre quando esse número é igual a 1.
Veja se consegue continuar a resolver a questão.
.


Agora, uma dica:e
são inversos um do outro e o menor valor da soma de um número com o seu inverso ocorre quando esse número é igual a 1.
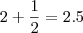 ,
, 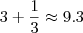 e assim por diante. Ou seja o menor valor da soma de um número por seu inverso ocorre quando o número é igual a 1.
e assim por diante. Ou seja o menor valor da soma de um número por seu inverso ocorre quando o número é igual a 1. deve ser igual a 1
deve ser igual a 1 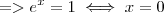 .
.  .
. .
.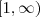 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: