 por Thulio_Parazi » Ter Abr 10, 2012 14:37
por Thulio_Parazi » Ter Abr 10, 2012 14:37
Seja a ? R tal que log2(a – 2) > 2. Tomando-se m = log2(a2 – 4),
então, é correto afirmar que m é
não conseguir desempenhar nada dessa questão.
Não sei o que fazer.
-
Thulio_Parazi
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qui Abr 05, 2012 11:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por fraol » Ter Abr 10, 2012 21:03
por fraol » Ter Abr 10, 2012 21:03
Note que
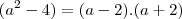
(esse é um produto notável).
Então

(log do produto é a soma dos logs).
Como

, o que você pode concluir a respeito de m ?
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Thulio_Parazi » Ter Abr 10, 2012 23:23
por Thulio_Parazi » Ter Abr 10, 2012 23:23
fraol escreveu:Note que
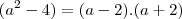
(esse é um produto notável).
Então

(log do produto é a soma dos logs).
Como

, o que você pode concluir a respeito de m ?
.
M >5 é isso, mas por que?
Não entendi.
-
Thulio_Parazi
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qui Abr 05, 2012 11:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por fraol » Qua Abr 11, 2012 00:34
por fraol » Qua Abr 11, 2012 00:34
Como

, pela definição de logaritmo você tem que:
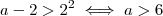
Agora vamos analisar

, como
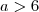
, então

.
No pior caso digamos que

, então
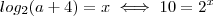
, 10 é aproximadamente

,
Assim
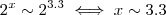
.
A soma que encontramos, o

contém uma parcela maior do que 2 e uma parcela maior do que 3.3. Portanto
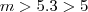
.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Thulio_Parazi » Qua Abr 11, 2012 12:56
por Thulio_Parazi » Qua Abr 11, 2012 12:56
fraol escreveu:Como

, pela definição de logaritmo você tem que:
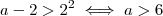
Agora vamos analisar

, como
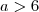
, então

.
No pior caso digamos que

, então
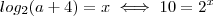
, 10 é aproximadamente

,
Assim
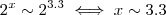
.
A soma que encontramos, o

contém uma parcela maior do que 2 e uma parcela maior do que 3.3. Portanto
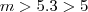
.
.
Valeu fraol,Kara você é fera, valeu mesmo de coração pela força e pela moral.
Com sua ajuda estou começando a ter mais esperança em passar.. Um abraço
-
Thulio_Parazi
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qui Abr 05, 2012 11:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Thulio_Parazi » Qui Abr 12, 2012 09:26
por Thulio_Parazi » Qui Abr 12, 2012 09:26
Me ajude nessa questão:viewtopic.php?f=111&t=7854
valeu
-
Thulio_Parazi
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qui Abr 05, 2012 11:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- cefet-mg 2012
por Thulio_Parazi » Ter Abr 10, 2012 09:55
- 1 Respostas
- 1605 Exibições
- Última mensagem por MarceloFantini

Ter Abr 10, 2012 21:12
Trigonometria
-
- Questão CEFET-MG 2012
por Thulio_Parazi » Qui Abr 05, 2012 13:48
- 5 Respostas
- 4835 Exibições
- Última mensagem por fraol

Ter Abr 10, 2012 20:02
Trigonometria
-
- Cefet-mg 2012 questão 03
por Thulio_Parazi » Sex Abr 13, 2012 11:12
- 4 Respostas
- 4495 Exibições
- Última mensagem por fraol

Qua Abr 18, 2012 22:26
Logaritmos
-
- Questão CEFET-MG graduação 2012
por Thulio_Parazi » Qui Abr 05, 2012 11:24
- 1 Respostas
- 2138 Exibições
- Última mensagem por fraol

Sex Abr 06, 2012 20:54
Trigonometria
-
- cefet-mg
por Thulio_Parazi » Ter Abr 10, 2012 10:06
- 2 Respostas
- 2427 Exibições
- Última mensagem por Thulio_Parazi

Seg Abr 16, 2012 11:50
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



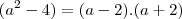

 , o que você pode concluir a respeito de m ?
, o que você pode concluir a respeito de m ?
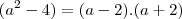

, o que você pode concluir a respeito de m ?

 , pela definição de logaritmo você tem que:
, pela definição de logaritmo você tem que: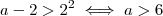
 , como
, como 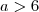 , então
, então  .
. , então
, então 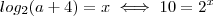 , 10 é aproximadamente
, 10 é aproximadamente  ,
,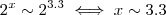 .
. contém uma parcela maior do que 2 e uma parcela maior do que 3.3. Portanto
contém uma parcela maior do que 2 e uma parcela maior do que 3.3. Portanto 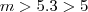 .
.
, pela definição de logaritmo você tem que:
, como
, então
.
, então
, 10 é aproximadamente
,
.
contém uma parcela maior do que 2 e uma parcela maior do que 3.3. Portanto
.


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
