é
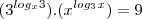 o número n. O valor de n é igual a:
o número n. O valor de n é igual a:(A) 1
(B) 3
(C) 9
(D) 27
Por favor!!!Tentei e não consegui!!!Obrigada!!

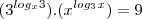 o número n. O valor de n é igual a:
o número n. O valor de n é igual a:
Pri Ferreira escreveu:O produto das 3 raízes da equaçãoé o número n. O valor de n é igual a:
(A) 1
(B) 3
(C) 9
(D) 27
Pri Ferreira escreveu: Por favor!!! Tentei e não consegui!!
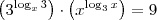
![\log_3 \left[\left({3}^{\log_x 3}\right)\cdot \left(x^{\log_3 x}\right)\right] = \log_3 9 \log_3 \left[\left({3}^{\log_x 3}\right)\cdot \left(x^{\log_3 x}\right)\right] = \log_3 9](/latexrender/pictures/8a8f22bdfc00d9bbde94f117357a2445.png)
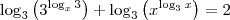
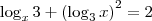
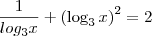
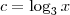 , temos que:
, temos que: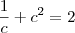
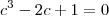
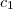 ,
, 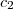 e
e 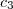 .
.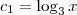 ,
, 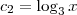 e
e 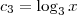 .
.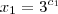 ,
, 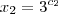 e
e 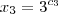 . Basta então calcular o produto entre essas soluções.
. Basta então calcular o produto entre essas soluções.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: