 por andersontricordiano » Qui Jan 12, 2012 13:06
por andersontricordiano » Qui Jan 12, 2012 13:06
Para que valores de m a equação
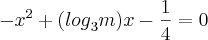
, na variável x apresenta duas raízes?
Resposta:
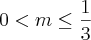
ou

-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por ant_dii » Qui Jan 12, 2012 14:32
por ant_dii » Qui Jan 12, 2012 14:32
Faça assim...
Primeiro escreva
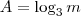
.
Daí
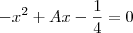
.
Por Bhaskara, teremos
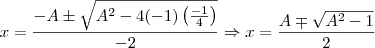
Esta equação somente terá duas equações quando
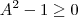
de onde
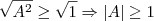
que implica em
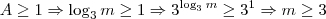
ou
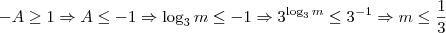
.
Como

é definido somente para números positivos deve-se ter
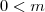
.
Portanto,
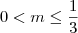
ou

.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UF-MG) Calcule o valor de A3/A2 do triângulo abaixo
 por andersontricordiano » Qua Mar 09, 2011 13:04
por andersontricordiano » Qua Mar 09, 2011 13:04
- 1 Respostas
- 2385 Exibições
- Última mensagem por andersontricordiano

Qua Mar 16, 2011 12:19
Geometria
-
- Calcule a matriz formada pelos coeficientes abaixo
por andersontricordiano » Qua Jan 04, 2012 15:52
- 1 Respostas
- 4751 Exibições
- Última mensagem por Arkanus Darondra

Qua Jan 04, 2012 20:23
Matrizes e Determinantes
-
- Calcule a equação
por andersontricordiano » Seg Fev 10, 2014 14:48
- 1 Respostas
- 1870 Exibições
- Última mensagem por Russman

Ter Fev 11, 2014 00:09
Funções
-
- Calcule o valor de m na equação matricial A*X=B
por andersontricordiano » Seg Jan 16, 2012 19:46
- 3 Respostas
- 3832 Exibições
- Última mensagem por Arkanus Darondra

Qua Jan 18, 2012 23:52
Matrizes e Determinantes
-
- Calcule dy/dx para y satisfazendo a equação y² + yx + x³ = 7
por Gzwrkk » Qua Dez 16, 2020 12:48
- 1 Respostas
- 3185 Exibições
- Última mensagem por DanielFerreira

Dom Mar 28, 2021 12:34
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
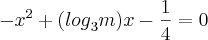 , na variável x apresenta duas raízes?
, na variável x apresenta duas raízes?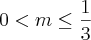 ou
ou 

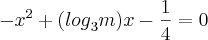 , na variável x apresenta duas raízes?
, na variável x apresenta duas raízes?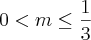 ou
ou 

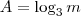 .
.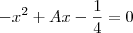 .
.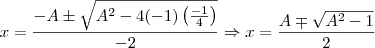
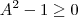 de onde
de onde 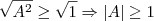 que implica em
que implica em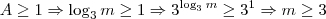
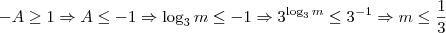 .
. é definido somente para números positivos deve-se ter
é definido somente para números positivos deve-se ter 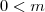 .
.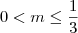 ou
ou  .
.