
consegui resolver da seguinte forma:
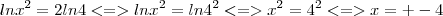
Ora, atendendo às soluções do caderno, esta é a solução certa. No entanto, tentei resolver doutra forma e deu outro resultado.
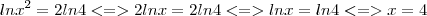
Alguém me sabe dizer onde está o erro ? obrigado


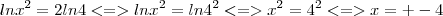
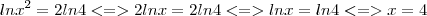

 ficamos com o x negativo, e pela propriedade de logaritmo nao é possivel.
ficamos com o x negativo, e pela propriedade de logaritmo nao é possivel.

molina escreveu:Boa tarde, Miguel.
Na verdade, a solução é apenas 4 pelo meu entendimento. Pois o logaritmando (x, no caso) precisa ser maior que zero. É claro que elevando -4 ao quadrado, tambem temos um numero positivo, porem, tendo x = -4, quando fazemosficamos com o x negativo, e pela propriedade de logaritmo nao é possivel.
Estou a disposiçao para mais questionamentos.
Bom estudo!
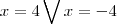 , e um dos exercícios é explicar porque não é só x=4.
, e um dos exercícios é explicar porque não é só x=4. molina escreveu: tendo x = -4, quando fazemosficamos com o x negativo, e pela propriedade de logaritmo nao é possivel.
 Poderá o número par continuar a exercer no logaritmando o efeito da exponenciação par, transformando-o em positivo ?
Poderá o número par continuar a exercer no logaritmando o efeito da exponenciação par, transformando-o em positivo ? 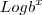 . Caso x fosse par, eu antes deduzia que o b podia ser negativo. Com esta sua explicação, o b NUNCA pode ser negativo, mesmo que o x seja par.
. Caso x fosse par, eu antes deduzia que o b podia ser negativo. Com esta sua explicação, o b NUNCA pode ser negativo, mesmo que o x seja par. 
 ). Mas quando faz o primeiro passo da sua resolução fica com o domínio da nova equação reduzido aos números positivos (porque só pode calcular
). Mas quando faz o primeiro passo da sua resolução fica com o domínio da nova equação reduzido aos números positivos (porque só pode calcular 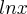 para valores de x positivos). Portanto o erro está logo no primeiro passo. Pense nisso. Será que pode mexer naquele expoente em qualquer caso?
para valores de x positivos). Portanto o erro está logo no primeiro passo. Pense nisso. Será que pode mexer naquele expoente em qualquer caso?
Sandra Piedade escreveu:Portanto o erro está logo no primeiro passo.



Sandra Piedade escreveu:Sim, é a esse passo que me refiro, penso que é aí que está o erro. Por isso só dá uma das duas soluções. Há que ter cuidado quando nos livramos de expoentes pares.



Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante