 por andersontricordiano » Dom Abr 10, 2011 23:11
por andersontricordiano » Dom Abr 10, 2011 23:11
Se ![\sqrt[]{{9}^{p+1}}={3}^{\sqrt[]{2}} \sqrt[]{{9}^{p+1}}={3}^{\sqrt[]{2}}](/latexrender/pictures/e0811a3dd72f63828255727507f80207.png)


,
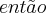

é igual a:
Detalhe a resposta é:7
Eu fiz eu não deu essa resposta!
Por favor resolvem esse calculo!
Obrigado quem resolver!
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Aliocha Karamazov » Seg Abr 11, 2011 02:02
por Aliocha Karamazov » Seg Abr 11, 2011 02:02
Olá, andersontricordiano. Vamos lá...
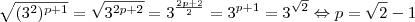
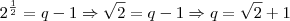

Agora, é só você fazer o desenvolvimento algébrico. Dica: utilize produto notável e diferença de quadrados.
Falou...
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo de logaritmos
por andersontricordiano » Sáb Mar 19, 2011 14:46
- 1 Respostas
- 1613 Exibições
- Última mensagem por MarceloFantini

Sáb Mar 19, 2011 15:06
Logaritmos
-
- CALCULO DE LOGARITMOS
por andersontricordiano » Qui Abr 07, 2011 02:48
- 1 Respostas
- 3073 Exibições
- Última mensagem por maykinho

Sex Abr 29, 2011 12:04
Logaritmos
-
- (UPE-PE) Calculo de logaritmos
por andersontricordiano » Sex Abr 15, 2011 22:15
- 1 Respostas
- 2058 Exibições
- Última mensagem por MarceloFantini

Sex Abr 15, 2011 22:41
Logaritmos
-
- cálculo de logaritmos
por ezidia51 » Sex Mar 16, 2018 00:58
- 2 Respostas
- 3580 Exibições
- Última mensagem por ezidia51

Sex Mar 16, 2018 15:23
Logaritmos
-
- Cálculo de Limites com Logaritmos
 por EREGON » Qua Jan 14, 2015 12:28
por EREGON » Qua Jan 14, 2015 12:28
- 0 Respostas
- 1216 Exibições
- Última mensagem por EREGON

Qua Jan 14, 2015 12:28
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{{9}^{p+1}}={3}^{\sqrt[]{2}} \sqrt[]{{9}^{p+1}}={3}^{\sqrt[]{2}}](/latexrender/pictures/e0811a3dd72f63828255727507f80207.png)

 ,
, 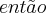
 é igual a:
é igual a:
![\sqrt[]{{9}^{p+1}}={3}^{\sqrt[]{2}} \sqrt[]{{9}^{p+1}}={3}^{\sqrt[]{2}}](/latexrender/pictures/e0811a3dd72f63828255727507f80207.png)

 ,
, 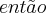
 é igual a:
é igual a:
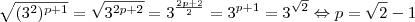
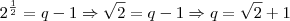


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.