 por Andersonborges » Sáb Fev 26, 2011 16:57
por Andersonborges » Sáb Fev 26, 2011 16:57
pessoal... comecei eng eletrica e to com muitas dificuldades em matematica basica... ao desenvolver do curso... conto com ajuda de todos.
para começar!
A resolução real para equação

, com a>0,

e B>0, e dada por?
nao to conseguindo nem incia equação

-
Andersonborges
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qui Fev 24, 2011 02:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por Molina » Sáb Fev 26, 2011 18:09
por Molina » Sáb Fev 26, 2011 18:09
Boa noite, Anderson.
Apareceu x no expoente uma das saídas é usar logaritmo:
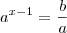
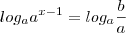
Pelas propriedades dos logaritmos, temos que:


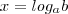
Pronto! Talvez você precise revisar as propriedades de logaritmos para compreender melhor o que foi feito. São propriedades simples e você vai se lembrar tranquilamente.
Conte conosco sempre que precisar.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizAquino » Sáb Fev 26, 2011 19:19
por LuizAquino » Sáb Fev 26, 2011 19:19
Dê uma olhada no tópico abaixo. Acredito que vai lhe ser útil.
Aulas de Matemática no YouTubeviewtopic.php?f=120&t=3818
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Andersonborges » Sáb Fev 26, 2011 20:46
por Andersonborges » Sáb Fev 26, 2011 20:46
mto obrigado... isso me ajudo mto
-
Andersonborges
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qui Fev 24, 2011 02:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por Andersonborges » Seg Fev 28, 2011 19:26
por Andersonborges » Seg Fev 28, 2011 19:26
a resposta esta errada conforme minha apostila... o correto eh

(b)-2
-
Andersonborges
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qui Fev 24, 2011 02:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por Molina » Seg Fev 28, 2011 19:38
por Molina » Seg Fev 28, 2011 19:38
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Andersonborges » Qui Mar 03, 2011 00:11
por Andersonborges » Qui Mar 03, 2011 00:11
amigo.. o erro foi meu... eu troquei um sinal.. A é liverado a x+1 e nao a x-1
-
Andersonborges
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qui Fev 24, 2011 02:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por Molina » Qui Mar 03, 2011 00:18
por Molina » Qui Mar 03, 2011 00:18
Andersonborges escreveu:amigo.. o erro foi meu... eu troquei um sinal.. A é liverado a x+1 e nao a x-1
Resolvido então, Anderson!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- logaritimos..
por lizbortolli » Sáb Nov 20, 2010 00:07
- 4 Respostas
- 3586 Exibições
- Última mensagem por Lorettto

Seg Dez 20, 2010 14:59
Logaritmos
-
- continuando com logaritimos
por Andersonborges » Sáb Fev 26, 2011 17:10
- 1 Respostas
- 1437 Exibições
- Última mensagem por Molina

Sáb Fev 26, 2011 18:27
Logaritmos
-
- Equação de logarítimos
por lilianers » Sex Mar 29, 2013 21:27
- 1 Respostas
- 1581 Exibições
- Última mensagem por young_jedi

Sáb Mar 30, 2013 11:54
Logaritmos
-
- Equação de logarítimos
por lilianers » Sex Mar 29, 2013 21:29
- 2 Respostas
- 2107 Exibições
- Última mensagem por lilianers

Sex Mar 29, 2013 22:08
Logaritmos
-
- LIMITES de exponenciais e logaritimos
por inkz » Qua Dez 05, 2012 16:13
- 1 Respostas
- 1692 Exibições
- Última mensagem por e8group

Qua Dez 05, 2012 20:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , com a>0,
, com a>0,  e B>0, e dada por?
e B>0, e dada por?

 , com a>0,
, com a>0,  e B>0, e dada por?
e B>0, e dada por?

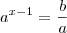
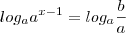


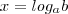




 (b)-2
(b)-2




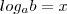






![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.