 por Jhenrique » Qui Set 13, 2012 02:50
por Jhenrique » Qui Set 13, 2012 02:50
Saudações!
Estive percebendo que certas calculadoras eletrônicas, inclusive o GeoGebra, chamam o módulo de x como uma função, abs(x)... então, por acaso cheguei a pensar: "e se de fato o módulo for uma função, será que é ou será que é apenas uma operação?"
Imaginei que se o módulo de fato fosse uma função, então ele teria uma inversa, x = abs?¹(y), que deveria ser igual a x = rel(y) e se existe uma função relativa, existe uma relativa inversa, que é igual a absoluta, rel?¹(x) = y, ou seja, abs(x) = y.
Em matemática pura, isso existe, está certo, faz sentido?
vlw,
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Qui Set 13, 2012 10:05
por MarceloFantini » Qui Set 13, 2012 10:05
Imaginei que se o módulo de fato fosse uma função, então ele teria uma inversa,[...]
Errado. Nem toda função tem inversa, apenas as que são bijetoras. Para que seja função, basta que cada ponto do domínio tenha uma única imagem no contradomínio (as imagens de dois elementos podem coincidir, mas um dado elemento NUNCA pode ter duas imagens!).
Além disso, toda operação é uma função. A operação de soma entre dois números reais, por exemplo, é uma função
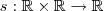
que recebe dois números reais e retorna outro por meio da soma, ou seja,

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Números primos e outras travas
por victorleme » Ter Mai 03, 2011 11:20
- 5 Respostas
- 4401 Exibições
- Última mensagem por victorleme

Qua Mai 04, 2011 00:54
Álgebra Elementar
-
- Algebra e outras - questões IFBA 2009
por Janffs » Seg Dez 24, 2012 01:07
- 1 Respostas
- 1888 Exibições
- Última mensagem por e8group

Seg Dez 24, 2012 11:30
Álgebra Elementar
-
- [RETAS] equação vetorial de reta que corta outras duas
por renan_a » Seg Out 01, 2012 19:32
- 3 Respostas
- 2030 Exibições
- Última mensagem por young_jedi

Seg Out 01, 2012 22:04
Geometria Analítica
-
- Funçao modular
por Fiel8 » Sex Jul 10, 2009 19:25
- 1 Respostas
- 2614 Exibições
- Última mensagem por Molina

Sex Jul 10, 2009 21:50
Funções
-
- Função Modular
 por geriane » Sáb Abr 03, 2010 21:32
por geriane » Sáb Abr 03, 2010 21:32
- 3 Respostas
- 3113 Exibições
- Última mensagem por Molina

Dom Abr 04, 2010 12:57
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


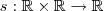 que recebe dois números reais e retorna outro por meio da soma, ou seja,
que recebe dois números reais e retorna outro por meio da soma, ou seja,  .
.
