[Função modular] Vestibular da UEPB 2012

[rickminick]

A soma das raízes que satisfazem a equação modular?
||x-2|-7|=6

Eu tentei tirar todo o módulo e fazer;
Fiz assim:
x-2-7=6 -----> x=15

A resposta realmente é quinze no gabarito, mas não entendi porque deveria somar as raízes e ainda falta tirar o módulo a equação sendo x-2<0. Acho que fiz errado

[fraol]

Boa noite,

Uma forma de resolver essa questão é, inicialmente, fazer .

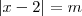Então . Então:

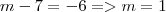
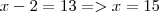
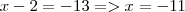
(a)

(b)

Agora utilizamos esses resultados para resolver .

Usando o resultado de (a):

(c)

(d)

Usando o resultado de (b):

(e)

(f)

Agora, finalizando, somamos as raizes: (c) + (d) + (e) + (f) = 8.

Veja, essa resposta não condiz que o gabarito que lhe forneceram. Creio que você deveria revisá-lo.

.

[rickminick]

É realmente olhei o gabarito errado, a chave dessa questão era isso mesmo |x-2|= m, revisei todo o assunto de módulo e nunca tinha visto questões assim, muito obrigado