 por Mariana Martin » Seg Jul 09, 2012 18:54
por Mariana Martin » Seg Jul 09, 2012 18:54
Olá, pessoal, não consigo entender porquê "a" é igual a -1, para mim a deveria ser igual a 1 positivo já que "a" é o termo independente. Me ajudem por favor.
Seja  em que a, b e c são números reais. A imagem de f é a semirreta ]?1,
em que a, b e c são números reais. A imagem de f é a semirreta ]?1,
?[ e o gráfico de f intercepta os eixos coordenados nos pontos (1, 0) e (0, ?3/4). Então,
o produto abc vale?
-
Mariana Martin
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qui Jun 21, 2012 15:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Seg Jul 09, 2012 19:25
por Russman » Seg Jul 09, 2012 19:25
Você possui 3 informação sobre a função. Monte um sistema, determine os parametros separadamente e , em seguida, efetue o produto.
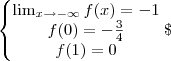
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Mariana Martin » Ter Jul 10, 2012 12:54
por Mariana Martin » Ter Jul 10, 2012 12:54
Desculpe, não entendi qual é o produto.
Tentei começar assim:

Mas ainda assim não consigo ver como posso chegar no a= -1
-
Mariana Martin
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qui Jun 21, 2012 15:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por 0 kelvin » Qua Jul 11, 2012 00:53
por 0 kelvin » Qua Jul 11, 2012 00:53
Conceito de limite é aplicável, mas como a fuvest não cobra limites:
Vou te dar uma dica: não tente um caminho só algébrico, pense nesse a = -1 de modo geométrico.
No papel ou em qualquer site ou programa de computador que faça gráficos de função, faça o gráfico desses três casos:



Agora veja o seguinte: vc deve saber que uma função exponencial da forma a^x, qualquer que seja o valor de
x e de
a a função não "encosta" no eixo x (não existe número elevado a outro que dê zero). Ou seja, a imagem é o intervalo ]0, oo[. Mas o enunciado diz que a imagem é o intervalo ]-1, oo[, oras, então o que a função tem que desloca todo o gráfico de uma unidade, tal que a função exponencial dada na questão tenha pontos na parte negativa do eixo y?
PS: a fuvest repete muito esse estilo, esta tudo lá dado e bem claro, mas se vc pula uma informação ou não entende direito, o problema fica insolúvel.
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
 por Mariana Martin » Qua Jul 11, 2012 12:36
por Mariana Martin » Qua Jul 11, 2012 12:36
Tudo bem, o termo independente faz com que a função "suba" ou "desça" em relação ao eixo das ordenadas (y), mas então, se a= -1 e o intervalo é ]-1;+

[, há a coordenada (0,0) ?
Isso não deveria ser impossível, como pode haver a coordenada (0,0)? Se
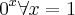
-
Mariana Martin
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qui Jun 21, 2012 15:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por 0 kelvin » Qua Jul 11, 2012 14:39
por 0 kelvin » Qua Jul 11, 2012 14:39
Lendo novamente a questão me saltou um outro detalhe:
A forma bx + c te lembra alguma coisa? É a forma de uma função afim. Pegue uma função por exemplo f(x) = 1x + c. O que acontece com a raiz dessa função quando o valor de c varia para mais e para menos? Vê um deslocamento no eixo x para a direita e para esquerda?
Parece que houve alguma confusão no quesito domínio e imagem da função se eu entendi direito a sua dúvida. A semireta dada no enunciado esta no eixo y. O domínio da função, que são todos os reais, esta no eixo x. Tanto no conjunto de valores do domínio quanto da imagem o valor zero existe, mas na função o ponto (0,0) não existe. Basta uma rápida observação para notar que se a função passa por (1,0) e (0, -3/4), ela não passa pela origem de jeito nenhum.
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
 por Mariana Martin » Qui Jul 12, 2012 13:18
por Mariana Martin » Qui Jul 12, 2012 13:18
Agora entendi a minha dúvida, só que não compreendi seu questionamento sobre o deslocamento para a esquerda ou direita se o "c" da função

aumentar ou diminuir.
se f(x)= Im(f) então o "c" não deveria fazer a função subir ou descer?
-
Mariana Martin
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qui Jun 21, 2012 15:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Qui Jul 12, 2012 13:47
por e8group » Qui Jul 12, 2012 13:47
Mariana Martin escreveu:Agora entendi a minha dúvida, só que não compreendi seu questionamento sobre o deslocamento para a esquerda ou direita se o "c" da função
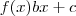
aumentar ou diminuir.
Note que " c " é o termo que intercepta o eixo y . Basta tomar f(0) e observa o mesmo . Assim f desloca (com a mesma direção) em relação ao eixo y a medida que c varia .
OBS.: Citei direção porque a inclinação da reta é independente do termo c .
Para você visualizar , imagine uma outra função , por exemplo :
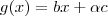
, onde

é um escalar . Fazendo uma analogia se g e f fosse uma reta r e s por exemplo teríamos duas retas paralelas . Pense assim ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qui Jul 12, 2012 15:41
por e8group » Qui Jul 12, 2012 15:41
santhiago escreveu:Agora entendi a minha dúvida, só que não compreendi seu questionamento sobre o deslocamento para a esquerda ou direita se o "c" da função f(x) = bx+c aumentar ou diminuir.
Mariana Martin escreveu:Note que " c " é o termo que intercepta o eixo y . Basta tomar f(0) e observa o mesmo . Assim f desloca (com a mesma direção) em relação ao eixo y a medida que c varia .
OBS.: Citei direção porque a inclinação da reta é independente do termo c .
Para você visualizar , imagine uma outra função , por exemplo : , onde é um escalar . Fazendo uma analogia se g e f fosse uma reta r e s por exemplo teríamos duas retas paralelas . Pense assim ...
Ah quero deixar bem claro que eu disse acima é verdadeiro se for uma função linear . ok .
em relação ao seu exercício ,

pelo enunciado sabemos que :

--------------------- i)

---------------------ii)
i) Temos que :

se e somente se

(porque ? Resposta: deixo a você refletir e chegar a conclusão ,ok. ) e
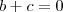
, ou seja :

.
ii)
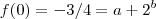
De i) em ii) obtemos :
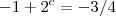
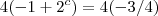





, portanto

Daí ,

-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação Exponencial(fuvest)
por gustavoluiss » Sex Mar 18, 2011 21:51
- 2 Respostas
- 2049 Exibições
- Última mensagem por gustavoluiss

Sex Mar 18, 2011 23:51
Funções
-
- gráfico exponencial
 por leticiapires52 » Ter Mai 13, 2014 13:53
por leticiapires52 » Ter Mai 13, 2014 13:53
- 0 Respostas
- 768 Exibições
- Última mensagem por leticiapires52

Ter Mai 13, 2014 13:53
Funções
-
- Exponencial gerado por gráfico do excel
por Catiani » Sáb Mar 31, 2012 11:00
- 0 Respostas
- 1720 Exibições
- Última mensagem por Catiani

Sáb Mar 31, 2012 11:00
Funções
-
- Fuvest-SP
por luanxd » Dom Fev 07, 2010 20:16
- 4 Respostas
- 5412 Exibições
- Última mensagem por luanxd

Ter Fev 09, 2010 11:06
Sistemas de Equações
-
- Fuvest
por CaAtr » Sex Abr 02, 2010 16:39
- 5 Respostas
- 4638 Exibições
- Última mensagem por Molina

Dom Abr 04, 2010 14:27
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 em que a, b e c são números reais. A imagem de f é a semirreta ]?1,
em que a, b e c são números reais. A imagem de f é a semirreta ]?1, 
 em que a, b e c são números reais. A imagem de f é a semirreta ]?1,
em que a, b e c são números reais. A imagem de f é a semirreta ]?1, 
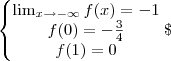







 [, há a coordenada (0,0) ?
[, há a coordenada (0,0) ?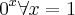


 aumentar ou diminuir.
aumentar ou diminuir.
aumentar ou diminuir.
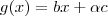 , onde
, onde  é um escalar . Fazendo uma analogia se g e f fosse uma reta r e s por exemplo teríamos duas retas paralelas . Pense assim ...
é um escalar . Fazendo uma analogia se g e f fosse uma reta r e s por exemplo teríamos duas retas paralelas . Pense assim ...

 --------------------- i)
--------------------- i)  ---------------------ii)
---------------------ii)  se e somente se
se e somente se  (porque ? Resposta: deixo a você refletir e chegar a conclusão ,ok. ) e
(porque ? Resposta: deixo a você refletir e chegar a conclusão ,ok. ) e 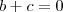 , ou seja :
, ou seja : .
.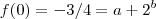
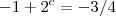
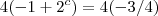




 , portanto
, portanto 

