O gráfico abaixo expressa a temperatura em graus Fahrenheit em função da temperatura em graus Celsius. Coloquei o link do exercício, pois não consegui passar o gráfico pra cá. Inclusive se alguém se dispuser a me explicar como faço isto. Tentei copiar e colar, mas não funcionou
http://www.pucrs.br/famat/mbotin/matema ... s20072.pdf
No gráfico, enquanto x=100 y=212 . Pensei em fazer: x=y-112. Só que não bate. Se eu considero que y =150 e faço X=150-112= X=38 não é correto. Pelo gráfico em y=150 x= 70
A segunda deu pra ver que y=32 enquanto x=0



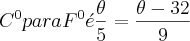 mas é uma fórmula aprendida, não extraida do gráfico como exige a questão.
mas é uma fórmula aprendida, não extraida do gráfico como exige a questão.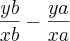 não tenho todos os dados, pois a questão fornece com precisão dois dados apenas da abcissa e da ordenada, que são (100,212). Eu não posso simplesmente traçar uma reta no gráfico e obter com exatidão os outros dois números que não foram fornecidos para complementar a fórmula. Vou tentar mais por aqui. Valeu a dica. Será que posso usar 0 e 32?
não tenho todos os dados, pois a questão fornece com precisão dois dados apenas da abcissa e da ordenada, que são (100,212). Eu não posso simplesmente traçar uma reta no gráfico e obter com exatidão os outros dois números que não foram fornecidos para complementar a fórmula. Vou tentar mais por aqui. Valeu a dica. Será que posso usar 0 e 32?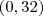 e o coeficiente angular é
e o coeficiente angular é  . Logo,
. Logo, 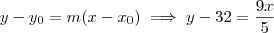 .
.



 , avisa que eu resolvo.
, avisa que eu resolvo.

