 por Andreza » Seg Nov 14, 2011 14:47
por Andreza » Seg Nov 14, 2011 14:47
Uma das raízes da equação
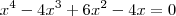
é (1+bi), onde i é uma unidade imaginária e b é um número real. Quais são as raízes dessa equação?
Como eu faço para calcular as raízes de uma equação do 4º Grau?
Obrigada.
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
 por MarceloFantini » Seg Nov 14, 2011 19:19
por MarceloFantini » Seg Nov 14, 2011 19:19
Se

é raíz da equação, então sabemos também que [ex]1-bi[/tex] também é raíz. Podemos colocar x em evidência no polinômio, logo zero também é raíz. Assim, podemos simplificar o polinômio como

, que pode ser fatorado como

, onde a é a raíz que queremos encontrar. Tente terminar agora.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8121 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
-
- Raízes da equação
por Andreza » Ter Nov 01, 2011 12:31
- 3 Respostas
- 1644 Exibições
- Última mensagem por Andreza

Ter Nov 01, 2011 18:04
Trigonometria
-
- Equação Raízes
por LuizCarlos » Seg Mai 07, 2012 13:59
- 2 Respostas
- 1384 Exibições
- Última mensagem por Cleyson007

Seg Mai 07, 2012 14:50
Álgebra Elementar
-
- Raízes da equação
 por joohhn » Qua Mai 18, 2016 17:11
por joohhn » Qua Mai 18, 2016 17:11
- 1 Respostas
- 1518 Exibições
- Última mensagem por joohhn

Qua Mai 18, 2016 20:46
Trigonometria
-
- equação de raízes complexas
por MariPC » Sáb Ago 15, 2009 15:56
- 1 Respostas
- 2217 Exibições
- Última mensagem por Felipe Schucman

Sáb Ago 15, 2009 17:35
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
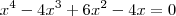

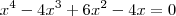

 é raíz da equação, então sabemos também que [ex]1-bi[/tex] também é raíz. Podemos colocar x em evidência no polinômio, logo zero também é raíz. Assim, podemos simplificar o polinômio como
é raíz da equação, então sabemos também que [ex]1-bi[/tex] também é raíz. Podemos colocar x em evidência no polinômio, logo zero também é raíz. Assim, podemos simplificar o polinômio como  , que pode ser fatorado como
, que pode ser fatorado como  , onde a é a raíz que queremos encontrar. Tente terminar agora.
, onde a é a raíz que queremos encontrar. Tente terminar agora.


 .
.
 :
: