Se
 e
e  , calcule o valor de
, calcule o valor de 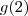 .
.
 e
e  , calcule o valor de
, calcule o valor de 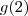 .
.
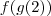
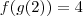
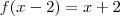
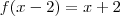
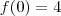
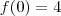 e
e 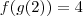 imagino eu que
imagino eu que 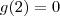
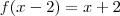
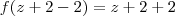
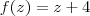
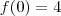 e
e 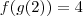 ...... =))
...... =))





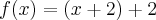
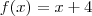
 basta substituir em
basta substituir em  e igualar a
e igualar a 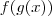
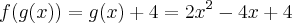
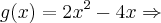 temos
temos 


Quando...

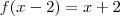 , podemos concluir que
, podemos concluir que  . Daí,
. Daí,  o que implica
o que implica 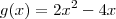 .
.


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

