 por IgorFilipe » Ter Ago 23, 2011 17:13
por IgorFilipe » Ter Ago 23, 2011 17:13
Bem galera, a materia parece ser muito facil (pontos notaveis de uma função quadratica), apenas com muitos calculos, mas parece ser bem fácil !
Eu gostaria de saber o que devo fazer nessa questão, já que Delta (ou discriminante) não tem Raiz quadrada
é a seguinte :
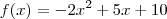
Que vai dar

-
IgorFilipe
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Ago 17, 2011 22:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Ter Ago 23, 2011 17:23
por Cleyson007 » Ter Ago 23, 2011 17:23
Boa tarde Igor!
O procedimento de resolução é o tradiconal mesmo. Veja:
f(x) = 2x² -5x - 10 (multipliquei por (-1) para eliminar o sinal negativo do termo a (x²)).
Quanto ao discriminante:
(-5)² - 4(2)(-10)
Delta = 105
Jogando em Bháskara:
- (-5) +/- V105 divido 2(2)
Resolvendo: x" = 5 + V105 / 4 e x" = 5 - V105 / 4
Qualquer dúvida informe no fórum.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por IgorFilipe » Ter Ago 23, 2011 20:18
por IgorFilipe » Ter Ago 23, 2011 20:18
Certo, então era so prosseguir com o 105.
Mas depois de achar x' e x'' eu tenho de fazer a Tabela de "x" e de "y" e depois o eixo de Simetria e o Y do vertice
É bem complicadinho quando não se tem a raiz exata do delta

Se souber como terminar ela eu ficaria muito grato, mas amanha eu tenho aula de novo de matematica e pergunto ela, acredito que não seja só eu do turma que fiquei com essa duvida .
Obrigado pela rapidez na resposta
-
IgorFilipe
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Ago 17, 2011 22:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Qua Ago 24, 2011 00:08
por LuizAquino » Qua Ago 24, 2011 00:08
Cleyson007 escreveu:O procedimento de resolução é o tradiconal mesmo. Veja:
f(x) = 2x² -5x - 10 (multipliquei por (-1) para eliminar o sinal negativo do termo a (x²)).
 Cuidado
Cuidado 
A função
 não é a mesma que
não é a mesma que 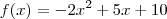
. Apesar delas possuírem as mesmas raízes, os seus gráficos são diferentes. Note que uma tem concavidade para baixo, enquanto que a outra para cima!
Você apenas poderia "multiplicar por (-1)" quando estivesse tratando com uma
equação. Ou seja, temos que
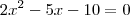
e
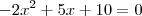
são equivalentes.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por IgorFilipe » Qua Ago 24, 2011 20:19
por IgorFilipe » Qua Ago 24, 2011 20:19
Parece que houve mesmo o engano no sinal .
Mas é concavidade para baixo mesmo, ou seja, o termo A é negativo mesmo.
Agora, ainda tenho a duvida, a maldita professora faltou hoje -.-'
Não sei como representar no grafico o x' e x''
-
IgorFilipe
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Ago 17, 2011 22:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Qua Ago 24, 2011 23:51
por LuizAquino » Qua Ago 24, 2011 23:51
IgorFilipe escreveu:(...) a maldita professora (...)
Não use esse tipo de linguagem! Respeite a sua professora e este fórum.
IgorFilipe escreveu:Não sei como representar no grafico o x' e x''
A ideia básica é calcular o valor aproximado de x' e x''.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por IgorFilipe » Sáb Ago 27, 2011 11:39
por IgorFilipe » Sáb Ago 27, 2011 11:39
Tá certo, a duvida já foi esclarecida.
Desculpe se falei daquele jeito, mas não foi na intenção de ódio ou raiva da professora, só uma palavra mesmo

-
IgorFilipe
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Ago 17, 2011 22:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Sáb Ago 27, 2011 13:07
por LuizAquino » Sáb Ago 27, 2011 13:07
IgorFilipe escreveu:Desculpe se falei daquele jeito, mas não foi na intenção de ódio ou raiva da professora, só uma palavra mesmo

Ok. Mas, procure tomar mais cuidado com o que você escreve ou fala.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Raiz Cúbica e Raiz Quadrada] Muito difícil achar a solução.
por Leocondeuba » Sáb Mai 11, 2013 19:27
- 2 Respostas
- 7458 Exibições
- Última mensagem por Leocondeuba

Sáb Mai 11, 2013 20:42
Aritmética
-
- Raiz quadrada
por j1a4l0 » Qui Abr 22, 2010 18:05
- 5 Respostas
- 5993 Exibições
- Última mensagem por Neperiano

Sex Abr 23, 2010 09:35
Funções
-
- raiz quadrada
por jose henrique » Seg Ago 16, 2010 16:54
- 1 Respostas
- 2348 Exibições
- Última mensagem por MarceloFantini

Ter Ago 17, 2010 00:03
Álgebra Elementar
-
- [Raiz quadrada de 13] Na mão
por Mickdark » Dom Abr 08, 2012 20:00
- 4 Respostas
- 17641 Exibições
- Última mensagem por Mickdark

Qui Abr 12, 2012 09:56
Álgebra Elementar
-
- Raiz quadrada
por anneliesero » Qua Dez 12, 2012 19:26
- 1 Respostas
- 2089 Exibições
- Última mensagem por replay

Qua Dez 19, 2012 16:11
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
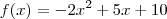


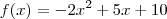




 não é a mesma que
não é a mesma que 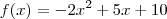 . Apesar delas possuírem as mesmas raízes, os seus gráficos são diferentes. Note que uma tem concavidade para baixo, enquanto que a outra para cima!
. Apesar delas possuírem as mesmas raízes, os seus gráficos são diferentes. Note que uma tem concavidade para baixo, enquanto que a outra para cima!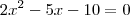 e
e 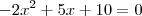 são equivalentes.
são equivalentes.









