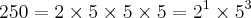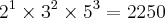por Cintra » Sáb Ago 13, 2011 14:25
por Cintra » Sáb Ago 13, 2011 14:25
Olá, nunca fui boa em matemática. Agora voltei a estudar e tenho alguns problemas para resolver.
Já entendi como encontrar o MMC, mas como faço para encontrar se tenho números muito grandes, Exp. 250, 450?
Se fosse o 15 = 3,5, certo?
Se fosse o 30 = 5,6, certo?
E de 250? 450? Começo por onde?
Vi que a resposta é 2250.
Pensei se a resposta é 2250 então devo encontrar o MMC pegando os 250 e 450 e dividindo por um número que o resultado seja inteiro.
Peguei 250 e dividi por 5 o MMC = 5, 50
Peguei 450 e dividi por 5 o MMC= = 5, 90
Peguei o 5 x 50 x 90 = 2250. Cheguei no resultado. Mas.... meu raciocínio esta certo? É assim que devo fazer?

Muito obrigada.
-
Cintra
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Ago 13, 2011 13:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: adm
- Andamento: formado
 por Caradoc » Sáb Ago 13, 2011 16:25
por Caradoc » Sáb Ago 13, 2011 16:25
Você pode fazer o processo da decomposição simultânea.
250 450 | 2
125 225 | 3
125 75 | 3
125 25 | 5
25 5 | 5
5 1 | 5
1 1
Coloque os números lado a lado e vá dividindo ambos pelos números primos (2,3,5,7,11..).
Caso uma das divisões não seja inteira, apenas copie tal número na próxima linha. Caso ambas as divisões não sejam inteiras, passe para o próximo primo.
No final, o mmc será o produto dos fatores primos.
Nesse caso, 2*3*3*5*5*5 = 2250
Outra maneira de encontrar, é listar os múltiplos de ambos os números, até achar o menor múltiplo comum:
250 => 250, 500, 750, 1000, 1250, 1500, 1750, 2000, 2250, 2500, 2750..
450 => 450, 900, 1350, 1800, 2250, 2700...
Como visto, o menor múltiplo comum entre 250 e 450 é 2250.
-
Caradoc
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qui Dez 16, 2010 17:17
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Cintra » Sáb Ago 13, 2011 16:50
por Cintra » Sáb Ago 13, 2011 16:50
Muito obrigada Caradoc!!!!

-
Cintra
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Ago 13, 2011 13:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: adm
- Andamento: formado
 por Gustavo R » Sáb Ago 13, 2011 17:21
por Gustavo R » Sáb Ago 13, 2011 17:21
Na verdade ñ é assim que se procede, Cintra. Isto que vc fez nem possui uma forma coerente que nos leve a desenvolver uma lógica. E 5 x 50 x 90 = 22500 e ñ 2250 que é a resposta correta. Mas ñ se preucupe quanto ao seu déficit em matemática, o importante é que vc comece a praticá-la bastante para que vc possa suprir suas dúvidas.Se vale uma dica, nunca passe para a próxima matéria antes de ter entendido bem a primeira. Bom vamos lá, o entendimento é simples: Para calcular o mínimo múltiplo comum entre dois ou mais números, devemos tomá-los por uma regrinha, sendo que independente da extenção do número, procedemos da mesma forma. Podemos calculá-lo de duas maneiras:
1) Pelo método da decomposição em fatores primos, fatoramos os números em questão que no caso são 250 e 450, separadamente até obtermos de cada um um produto de fatores PRIMOS:
a)
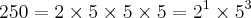

b) em seguida multiplicamos os fatores comuns e os não comuns dos numeros em questão, tomando os fatores com os MAIORES expoentes:
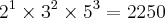
2) e a segunda maneira de se calcular o mmc é juntar todos os números separando-os por vírgula e dividí-los por fatores primos ( menores natutais possíveis); quando chegar ao ponto em que um número ñ dividi pelo mesmo fator que dividi o outro, repita-o na linha de baixo até que ele divida pelo mesmo fator que o outro e vice-versa. Quando os números chegarem na decomposição final com o fator 1, a fatoração estará terminada, e assim basta multiplicar os fatoter primos da direita e obteremos o mínimo múltiplo comum dos números fatorados. A esse método chamamos de decomposição simultânea.
250, 450 I 2
125, 225 I 3
125,..75 I 3
125,..25 I 5
25,.....5 I 5
5,......1 I 5/


1,......1 I
-
Gustavo R
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Ago 12, 2011 19:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Inequaçoes Exponenciais] Grandes Dificuldades
por R0nny » Sáb Mai 11, 2013 20:47
- 0 Respostas
- 702 Exibições
- Última mensagem por R0nny

Sáb Mai 11, 2013 20:47
Equações
-
- Função para descobrir primos grandes (200 dígitos ou +)
por imaia » Qui Set 06, 2012 17:56
- 2 Respostas
- 2632 Exibições
- Última mensagem por Renato_RJ

Sex Set 07, 2012 04:37
Funções
-
- [Teoria Números] Algoritmo Não Interceptação Números Primos
por WillamesSilva » Qua Out 26, 2016 12:21
- 8 Respostas
- 17193 Exibições
- Última mensagem por WillamesSilva

Ter Nov 22, 2016 15:33
Aritmética
-
- LEC - encontrar valores
por Washington Murakami » Dom Out 09, 2011 21:55
- 1 Respostas
- 1208 Exibições
- Última mensagem por Washington Murakami

Dom Out 09, 2011 21:59
Matemática Financeira
-
- P.G. (Encontrar os termos)
por Rafael16 » Qua Jul 18, 2012 23:15
- 1 Respostas
- 2505 Exibições
- Última mensagem por Russman

Qui Jul 19, 2012 00:02
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.