Estou com dúvidas nesta questão e não sei como resolver:
Um objeto é lançado obliquamente paracima, segundo a trajetória dada pela função
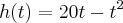 , em que h representa a altura em metros atingida pelo objeto, e t o tempo dado em segundos. A altura máxima que esse objeto pode atingir, em metros, é igual a:
, em que h representa a altura em metros atingida pelo objeto, e t o tempo dado em segundos. A altura máxima que esse objeto pode atingir, em metros, é igual a:Não sei a resposta...
Agradeço quem puder me ajudar.
Obrigado!




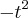 acredito que seja uma curva para baixo...
acredito que seja uma curva para baixo...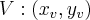
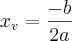
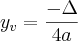

 e o
e o  , aconselho fazer um esboço do gráfico, o que irá facilitar ainda mais o entendimento da questão.
, aconselho fazer um esboço do gráfico, o que irá facilitar ainda mais o entendimento da questão.
 é uma função de
é uma função de  , ela é decrescente apenas quando
, ela é decrescente apenas quando 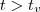 .
.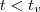 .
.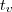 a abscissa do ponto de máximo.
a abscissa do ponto de máximo.