 por Caroline Oliveyra » Ter Jul 12, 2011 22:18
por Caroline Oliveyra » Ter Jul 12, 2011 22:18
Eu again!

Tem uma questão aki numa das minhas listas que dá a lei da função
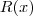
=
![\sqrt[2]{\frac{13 + 7x^\left(0.4 \right)}{1 + 4x^\left(0.4 \right)}} \sqrt[2]{\frac{13 + 7x^\left(0.4 \right)}{1 + 4x^\left(0.4 \right)}}](/latexrender/pictures/159e6409e022fb3eadc44a5dcdbce99f.png)
(feio né?) Enfim. Primeiro pede para calcular

que é tranquilo:
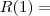
![\sqrt[2]{\frac{13 + 7.1^\left(0.4 \right)}{1 + 4.1^\left(0.4 \right)}} \sqrt[2]{\frac{13 + 7.1^\left(0.4 \right)}{1 + 4.1^\left(0.4 \right)}}](/latexrender/pictures/c3714a93446717a0a1724dfb8bd45e72.png)

![\sqrt[2]{\frac{20}{5}} \sqrt[2]{\frac{20}{5}}](/latexrender/pictures/7063ceacb2ee959d9922df76e52a797f.png)

![\sqrt[2]{4} = 2 \sqrt[2]{4} = 2](/latexrender/pictures/9bd863e5bae20c42d59d09884f7e4ab7.png)
Depois pede pra calcular o
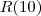
e o

. Eu boiei Tentei de todos os jeitos que eu pude imaginar, mas nem deu...

Nos dois casos passei

e
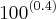
para
![\sqrt[4]{10^\left(10 \right)} \sqrt[4]{10^\left(10 \right)}](/latexrender/pictures/e07c4cefa4f9ffffe13bd10c55b8e830.png)
e
![\sqrt[4]{100^\left(10 \right)} \sqrt[4]{100^\left(10 \right)}](/latexrender/pictures/1524c04aee4d79fe15e2c2ab835ce2fa.png)
respectivamente... Mas ficou pior ainda, complicou.
Quem puder me ajudar eu já agradeço [MUITO]!!

Beijinhos!!!
"... então não importa se você é antílope ou leão; amanheceu, comece a correr."
-
Caroline Oliveyra
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Jun 19, 2011 13:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Metalúrgica e de Materiais
- Andamento: cursando
 por MarceloFantini » Qua Jul 13, 2011 04:11
por MarceloFantini » Qua Jul 13, 2011 04:11
Tome cuidado:
![10^{0.4} = 10^{\frac{4}{10}} = \sqrt[10]{10^4} 10^{0.4} = 10^{\frac{4}{10}} = \sqrt[10]{10^4}](/latexrender/pictures/b41a690c731f55436bd19b1131f84fd7.png)
e não
![\sqrt[4]{10^{10}} \sqrt[4]{10^{10}}](/latexrender/pictures/68a2f429bd5f8a0fd0cfe42d9ecebb3f.png)
. A uma primeira vista aparentemente não há simplificações e o jeito é usar calculadora mesmo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- tem como resolver sem utilizar a calculadora
por weverton » Sex Jun 25, 2010 03:38
- 2 Respostas
- 1805 Exibições
- Última mensagem por weverton

Sáb Jun 26, 2010 04:12
Matemática Financeira
-
- tem como resolver isso sem usar calculadora?
por weverton » Sáb Jul 24, 2010 06:07
- 3 Respostas
- 2308 Exibições
- Última mensagem por Neperiano

Seg Jul 26, 2010 00:36
Geometria Plana
-
- como fazer?
por Amandatkm » Qui Mar 21, 2013 18:12
- 1 Respostas
- 2446 Exibições
- Última mensagem por timoteo

Qui Mar 21, 2013 20:56
Geometria Espacial
-
- não sei como fazer!!
por Lenin » Seg Jun 10, 2013 11:29
- 0 Respostas
- 1927 Exibições
- Última mensagem por Lenin

Seg Jun 10, 2013 11:29
Polinômios
-
- [Diagonalização] Como fazer?
por Alvadorn » Sáb Nov 10, 2012 17:12
- 1 Respostas
- 3002 Exibições
- Última mensagem por MarceloFantini

Sáb Nov 10, 2012 18:43
Álgebra
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
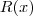 =
= ![\sqrt[2]{\frac{13 + 7x^\left(0.4 \right)}{1 + 4x^\left(0.4 \right)}} \sqrt[2]{\frac{13 + 7x^\left(0.4 \right)}{1 + 4x^\left(0.4 \right)}}](/latexrender/pictures/159e6409e022fb3eadc44a5dcdbce99f.png) (feio né?) Enfim. Primeiro pede para calcular
(feio né?) Enfim. Primeiro pede para calcular  que é tranquilo:
que é tranquilo: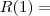
![\sqrt[2]{\frac{13 + 7.1^\left(0.4 \right)}{1 + 4.1^\left(0.4 \right)}} \sqrt[2]{\frac{13 + 7.1^\left(0.4 \right)}{1 + 4.1^\left(0.4 \right)}}](/latexrender/pictures/c3714a93446717a0a1724dfb8bd45e72.png)

![\sqrt[2]{\frac{20}{5}} \sqrt[2]{\frac{20}{5}}](/latexrender/pictures/7063ceacb2ee959d9922df76e52a797f.png)

![\sqrt[2]{4} = 2 \sqrt[2]{4} = 2](/latexrender/pictures/9bd863e5bae20c42d59d09884f7e4ab7.png)
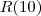 e o
e o  . Eu boiei Tentei de todos os jeitos que eu pude imaginar, mas nem deu...
. Eu boiei Tentei de todos os jeitos que eu pude imaginar, mas nem deu...  Nos dois casos passei
Nos dois casos passei  e
e 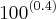 para
para ![\sqrt[4]{10^\left(10 \right)} \sqrt[4]{10^\left(10 \right)}](/latexrender/pictures/e07c4cefa4f9ffffe13bd10c55b8e830.png) e
e ![\sqrt[4]{100^\left(10 \right)} \sqrt[4]{100^\left(10 \right)}](/latexrender/pictures/1524c04aee4d79fe15e2c2ab835ce2fa.png) respectivamente... Mas ficou pior ainda, complicou.
respectivamente... Mas ficou pior ainda, complicou.


![10^{0.4} = 10^{\frac{4}{10}} = \sqrt[10]{10^4} 10^{0.4} = 10^{\frac{4}{10}} = \sqrt[10]{10^4}](/latexrender/pictures/b41a690c731f55436bd19b1131f84fd7.png) e não
e não ![\sqrt[4]{10^{10}} \sqrt[4]{10^{10}}](/latexrender/pictures/68a2f429bd5f8a0fd0cfe42d9ecebb3f.png) . A uma primeira vista aparentemente não há simplificações e o jeito é usar calculadora mesmo.
. A uma primeira vista aparentemente não há simplificações e o jeito é usar calculadora mesmo.
