 por jamiel » Dom Jun 26, 2011 16:40
por jamiel » Dom Jun 26, 2011 16:40
Usando loga 3 = 1,09, loga 2 = 0,69 ou loga 5 = 1,61, calcule o valor dos seguintes logaritmos:
a) loga 144
b) loga 7200
c) loga ?32
d) loga
![\sqrt[3]{600} \sqrt[3]{600}](/latexrender/pictures/4a5c48f57e4945456d4a2a5be9e89071.png)
e) loga 36*
![\sqrt[4]{18} \sqrt[4]{18}](/latexrender/pictures/1b0b88f4687231b81aa08b727d7efb33.png)
f) loga
![\frac{\sqrt[]{3}}{200} \frac{\sqrt[]{3}}{200}](/latexrender/pictures/044e47340969f2005e6027849543039b.png)
Alguém poderia resolver, pelo menos, uma para que eu possa entender esse conceito? Sinceramente, eu não sei por onde começar!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por LuizAquino » Dom Jun 26, 2011 16:49
por LuizAquino » Dom Jun 26, 2011 16:49
Você vai aplicar a mesma ideia usada no exercício do tópico:
Função Log - Tensoviewtopic.php?f=107&t=5197
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jamiel » Dom Jun 26, 2011 16:51
por jamiel » Dom Jun 26, 2011 16:51
Blza. Vou dar uma analisada aqui!
vlw ...
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por jamiel » Dom Jun 26, 2011 17:29
por jamiel » Dom Jun 26, 2011 17:29
Putz. É verdade, resolvi a letra a do mesmo jeito q naquele tópico
144/3 = 2 e 144/2 = 4
2,18 + 2,76 = 4,94
vlw
quero analisar o conceit, vou dar mais uma olhadinha aqui ...
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por jamiel » Dom Jun 26, 2011 21:52
por jamiel » Dom Jun 26, 2011 21:52
P utz. Voltei agora para o PC e deu uma pensada nessa da raiz quadrada de 32.
Seria assim?
![log (a, \sqrt[]{32})
\left({{2}^{5}}^{\frac{1}{2}} \right)
\left({2}^{\frac{5}{2}} \right)
\left(\frac{5}{2}*0,69 = 1,725 \right) log (a, \sqrt[]{32})
\left({{2}^{5}}^{\frac{1}{2}} \right)
\left({2}^{\frac{5}{2}} \right)
\left(\frac{5}{2}*0,69 = 1,725 \right)](/latexrender/pictures/b24675c13205f9ca5b0a178b430e6d12.png)
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Dom Jun 26, 2011 21:54
por MarceloFantini » Dom Jun 26, 2011 21:54
Exatamente. Parabéns!
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jamiel » Dom Jun 26, 2011 22:27
por jamiel » Dom Jun 26, 2011 22:27
Fiquei em dúvida nessa, mas eu acho q deu pra resolver!
![\left(log (a, \sqrt[3]{600})\right)
\left({600}^{\frac{1}{3}} \right)
\left(1,09 + 3*0,69 + 2*1,61\right)
\left(6,38 * \frac{1}{3} = 2,126\right) \left(log (a, \sqrt[3]{600})\right)
\left({600}^{\frac{1}{3}} \right)
\left(1,09 + 3*0,69 + 2*1,61\right)
\left(6,38 * \frac{1}{3} = 2,126\right)](/latexrender/pictures/69c4eb6b42511bd347ef14f2063e0b20.png)
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por jamiel » Dom Jun 26, 2011 23:32
por jamiel » Dom Jun 26, 2011 23:32
Fiquei confuso com essa:
![log (a, 36*\sqrt[4]{18})
\left(36:2, 36:3 = 2*0,69 + 2*1,09 = 3,56 \right)
\left(18:2, 18:3, 0,69 + 2*1,09 = \frac{2,87}{4} = 0,7175 \right)
3,56 + 0,7175 = 4,2775 log (a, 36*\sqrt[4]{18})
\left(36:2, 36:3 = 2*0,69 + 2*1,09 = 3,56 \right)
\left(18:2, 18:3, 0,69 + 2*1,09 = \frac{2,87}{4} = 0,7175 \right)
3,56 + 0,7175 = 4,2775](/latexrender/pictures/4f2c7eb0450176bf441fcb40bf6678cd.png)
Eu considerei uma das propriedades(em vez de multiplicar, somar!), será q tá certo?
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Dom Jun 26, 2011 23:39
por MarceloFantini » Dom Jun 26, 2011 23:39
Lembre-se que
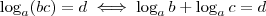
. Então:
![\log_a 36 \cdot \sqrt[4]{18} = \log_a 36 + \log_a \sqrt[4]{18} \log_a 36 \cdot \sqrt[4]{18} = \log_a 36 + \log_a \sqrt[4]{18}](/latexrender/pictures/fcdb0aa796ed4a09210d1556597cea9e.png)
Não consegui acompanhar sua solução, ficou um pouco confusa para mim, mas veja se o que você fez bate.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jamiel » Seg Jun 27, 2011 00:12
por jamiel » Seg Jun 27, 2011 00:12
rsrsrsr
Putz! Eu acho q o q vc fez tá mais certo q o meu, mas não sei como resolver isso q vc fez!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Seg Jun 27, 2011 00:18
por MarceloFantini » Seg Jun 27, 2011 00:18
Jamiel, agora ficou mais fácil, é só você calcular quanto dá cada logaritmo usando o que você fez anteriormente e somar.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função Log - Tenso
por jamiel » Qua Jun 22, 2011 15:49
- 2 Respostas
- 2063 Exibições
- Última mensagem por jamiel

Qua Jun 22, 2011 17:17
Funções
-
- Função Exponencial - Tenso!
por jamiel » Sáb Jun 18, 2011 03:12
- 4 Respostas
- 2542 Exibições
- Última mensagem por jamiel

Dom Jun 19, 2011 17:54
Funções
-
- Limite tenso
por Isabela Sa » Qua Jun 29, 2011 19:27
- 1 Respostas
- 1265 Exibições
- Última mensagem por Claudin

Qua Jun 29, 2011 19:51
Cálculo: Limites, Derivadas e Integrais
-
- Sisteminha tenso!!
por bigolasMan » Sex Mai 04, 2012 00:21
- 1 Respostas
- 1131 Exibições
- Última mensagem por Russman

Sex Mai 04, 2012 00:37
Sistemas de Equações
-
- Dúvida Função
por RJ1572 » Qui Abr 08, 2010 23:22
- 3 Respostas
- 2166 Exibições
- Última mensagem por Elcioschin

Sex Abr 09, 2010 13:22
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[3]{600} \sqrt[3]{600}](/latexrender/pictures/4a5c48f57e4945456d4a2a5be9e89071.png)
![\sqrt[4]{18} \sqrt[4]{18}](/latexrender/pictures/1b0b88f4687231b81aa08b727d7efb33.png)
![\frac{\sqrt[]{3}}{200} \frac{\sqrt[]{3}}{200}](/latexrender/pictures/044e47340969f2005e6027849543039b.png)

![\sqrt[3]{600} \sqrt[3]{600}](/latexrender/pictures/4a5c48f57e4945456d4a2a5be9e89071.png)
![\sqrt[4]{18} \sqrt[4]{18}](/latexrender/pictures/1b0b88f4687231b81aa08b727d7efb33.png)
![\frac{\sqrt[]{3}}{200} \frac{\sqrt[]{3}}{200}](/latexrender/pictures/044e47340969f2005e6027849543039b.png)




![log (a, \sqrt[]{32})
\left({{2}^{5}}^{\frac{1}{2}} \right)
\left({2}^{\frac{5}{2}} \right)
\left(\frac{5}{2}*0,69 = 1,725 \right) log (a, \sqrt[]{32})
\left({{2}^{5}}^{\frac{1}{2}} \right)
\left({2}^{\frac{5}{2}} \right)
\left(\frac{5}{2}*0,69 = 1,725 \right)](/latexrender/pictures/b24675c13205f9ca5b0a178b430e6d12.png)


![\left(log (a, \sqrt[3]{600})\right)
\left({600}^{\frac{1}{3}} \right)
\left(1,09 + 3*0,69 + 2*1,61\right)
\left(6,38 * \frac{1}{3} = 2,126\right) \left(log (a, \sqrt[3]{600})\right)
\left({600}^{\frac{1}{3}} \right)
\left(1,09 + 3*0,69 + 2*1,61\right)
\left(6,38 * \frac{1}{3} = 2,126\right)](/latexrender/pictures/69c4eb6b42511bd347ef14f2063e0b20.png)

![log (a, 36*\sqrt[4]{18})
\left(36:2, 36:3 = 2*0,69 + 2*1,09 = 3,56 \right)
\left(18:2, 18:3, 0,69 + 2*1,09 = \frac{2,87}{4} = 0,7175 \right)
3,56 + 0,7175 = 4,2775 log (a, 36*\sqrt[4]{18})
\left(36:2, 36:3 = 2*0,69 + 2*1,09 = 3,56 \right)
\left(18:2, 18:3, 0,69 + 2*1,09 = \frac{2,87}{4} = 0,7175 \right)
3,56 + 0,7175 = 4,2775](/latexrender/pictures/4f2c7eb0450176bf441fcb40bf6678cd.png)

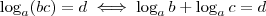 . Então:
. Então:![\log_a 36 \cdot \sqrt[4]{18} = \log_a 36 + \log_a \sqrt[4]{18} \log_a 36 \cdot \sqrt[4]{18} = \log_a 36 + \log_a \sqrt[4]{18}](/latexrender/pictures/fcdb0aa796ed4a09210d1556597cea9e.png)





![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.