 por renatofbc » Qua Jun 22, 2011 22:33
por renatofbc » Qua Jun 22, 2011 22:33
Não sei se é da hora, mas não consigo resolver esta equação, vai dar 3/2 (soluções) mas não consigo chegar lá.

Obrigado !
-
renatofbc
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Jun 22, 2011 22:17
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Ciência e Tecnologia
- Andamento: cursando
 por carlosalesouza » Qua Jun 22, 2011 23:15
por carlosalesouza » Qua Jun 22, 2011 23:15
Simples de tudo, meu caro... vamos manipulando algebricamente que a resposta aparece sozinha... rs

Certo?
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por MarceloFantini » Qua Jun 22, 2011 23:35
por MarceloFantini » Qua Jun 22, 2011 23:35
Quero atentar ao fato de que pode-se multiplicar tudo por
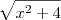
pois não existe x real tal que isto seja zero.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função Racional - preciso de ajuda para hoje ainda!
por raf » Seg Set 28, 2015 14:32
- 1 Respostas
- 2604 Exibições
- Última mensagem por nakagumahissao

Sex Out 02, 2015 00:47
Funções
-
- Ajuda Urgente com esse problema de função
por Mayedra » Ter Nov 17, 2015 16:33
- 0 Respostas
- 1636 Exibições
- Última mensagem por Mayedra

Ter Nov 17, 2015 16:33
Funções
-
- Contradominio de função racional
por joaofonseca » Dom Jul 03, 2011 11:54
- 9 Respostas
- 33330 Exibições
- Última mensagem por LuizAquino

Sex Fev 10, 2012 10:52
Funções
-
- Integral de função racional
por renan_a » Qua Jan 09, 2013 17:57
- 2 Respostas
- 1968 Exibições
- Última mensagem por renan_a

Qua Jan 09, 2013 22:05
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de Limite de Função Racional
por joaofonseca » Qua Mai 04, 2011 20:50
- 3 Respostas
- 2348 Exibições
- Última mensagem por LuizAquino

Qua Mai 04, 2011 23:53
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






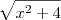 pois não existe x real tal que isto seja zero.
pois não existe x real tal que isto seja zero.
