 por jamiel » Sex Jun 17, 2011 16:24
por jamiel » Sex Jun 17, 2011 16:24
![\sqrt[5]{{3}^{2x}} = {2.187}^{\frac{{35x}^{2}-1}{35}}
{\left({3}^{\frac{2}{3}} \right)}^{x} = 7*\left(\frac{{35x}^{2}-1}{35} \right)
\left(\frac{2}{5}x \right) = \frac{{245x}^{2}- 7}{35}
\left(\frac{2}{5}x \right) = \frac{{35x}^{2}- 1}{5}
{-35x}^{2}:5 + (\left(\frac{2}{5} \right)x + \frac{1}{5})
{-7x}^{2} + (\left(\frac{2}{5} \right)x + \frac{1}{5})
\left(2:5*2:5 -4*(-7)*(1:5)\right)
4:25 -4*(-7:5)
\left(\frac{4}{25} \right)+\left(\frac{28}{5} \right)
\sqrt{\frac{140}{25}}
\left(\frac{2\sqrt[]{35}}{5} \right)
\left(\frac{\left-(\frac{2}{5} \right)x + \left(\frac{2\sqrt[]{35}}{5} \right)}{-14}\right)
\left(\frac{\left-(\frac{2}{5} \right)x - \left(\frac{2\sqrt[]{35}}{5} \right)}{-14}\right) \sqrt[5]{{3}^{2x}} = {2.187}^{\frac{{35x}^{2}-1}{35}}
{\left({3}^{\frac{2}{3}} \right)}^{x} = 7*\left(\frac{{35x}^{2}-1}{35} \right)
\left(\frac{2}{5}x \right) = \frac{{245x}^{2}- 7}{35}
\left(\frac{2}{5}x \right) = \frac{{35x}^{2}- 1}{5}
{-35x}^{2}:5 + (\left(\frac{2}{5} \right)x + \frac{1}{5})
{-7x}^{2} + (\left(\frac{2}{5} \right)x + \frac{1}{5})
\left(2:5*2:5 -4*(-7)*(1:5)\right)
4:25 -4*(-7:5)
\left(\frac{4}{25} \right)+\left(\frac{28}{5} \right)
\sqrt{\frac{140}{25}}
\left(\frac{2\sqrt[]{35}}{5} \right)
\left(\frac{\left-(\frac{2}{5} \right)x + \left(\frac{2\sqrt[]{35}}{5} \right)}{-14}\right)
\left(\frac{\left-(\frac{2}{5} \right)x - \left(\frac{2\sqrt[]{35}}{5} \right)}{-14}\right)](/latexrender/pictures/31bbfed4344375ec3c65b39e30099bf1.png)
Alguém poderia me ajudar quanto essa resolução?
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Sex Jun 17, 2011 17:13
por MarceloFantini » Sex Jun 17, 2011 17:13
Qual o enunciado, o que a questão pede e o que você tentou fazer?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jamiel » Sex Jun 17, 2011 23:10
por jamiel » Sex Jun 17, 2011 23:10
Apenas descobrir o valor de "x", ou seja, resolver a equação!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por jamiel » Sáb Jun 18, 2011 17:02
por jamiel » Sáb Jun 18, 2011 17:02
Ok. Quer dizer q eu poderia eliminar o denominador arbitrariamente? Eu sempre tendo ao caminho mais complicado! rsrsr
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Sáb Jun 18, 2011 17:15
por MarceloFantini » Sáb Jun 18, 2011 17:15
Não foi arbitrário. Note que se fosse

, por exemplo, a equação ficaria

. Basicamente o que eu fiz foi multiplicar os dois lados por 5, eliminando o denominador em comum.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jamiel » Sáb Jun 18, 2011 19:17
por jamiel » Sáb Jun 18, 2011 19:17
Então, quer dizer q sua multiplicação ficou assim:
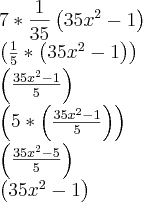
?
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Sáb Jun 18, 2011 19:34
por MarceloFantini » Sáb Jun 18, 2011 19:34
Apenas no lado direito sim, e a propósito você esqueceu de multiplicar o
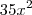
por 5 na penúltima linha.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jamiel » Sáb Jun 18, 2011 19:36
por jamiel » Sáb Jun 18, 2011 19:36
Ok. Vlw mesmo!
Tenho dificuldade com relação a essas reduções de termos!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Sáb Jun 18, 2011 19:53
por MarceloFantini » Sáb Jun 18, 2011 19:53
Acredito que seja mais fácil de enxergar se você entender aquele produto assim:

pois

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5574 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4590 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5745 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3485 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
-
- [FUNÇÃO] Não consigo achar a fórmula da função
por LAZAROTTI » Qui Set 27, 2012 00:06
- 1 Respostas
- 2955 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 07:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[5]{{3}^{2x}} = {2.187}^{\frac{{35x}^{2}-1}{35}}
{\left({3}^{\frac{2}{3}} \right)}^{x} = 7*\left(\frac{{35x}^{2}-1}{35} \right)
\left(\frac{2}{5}x \right) = \frac{{245x}^{2}- 7}{35}
\left(\frac{2}{5}x \right) = \frac{{35x}^{2}- 1}{5}
{-35x}^{2}:5 + (\left(\frac{2}{5} \right)x + \frac{1}{5})
{-7x}^{2} + (\left(\frac{2}{5} \right)x + \frac{1}{5})
\left(2:5*2:5 -4*(-7)*(1:5)\right)
4:25 -4*(-7:5)
\left(\frac{4}{25} \right)+\left(\frac{28}{5} \right)
\sqrt{\frac{140}{25}}
\left(\frac{2\sqrt[]{35}}{5} \right)
\left(\frac{\left-(\frac{2}{5} \right)x + \left(\frac{2\sqrt[]{35}}{5} \right)}{-14}\right)
\left(\frac{\left-(\frac{2}{5} \right)x - \left(\frac{2\sqrt[]{35}}{5} \right)}{-14}\right) \sqrt[5]{{3}^{2x}} = {2.187}^{\frac{{35x}^{2}-1}{35}}
{\left({3}^{\frac{2}{3}} \right)}^{x} = 7*\left(\frac{{35x}^{2}-1}{35} \right)
\left(\frac{2}{5}x \right) = \frac{{245x}^{2}- 7}{35}
\left(\frac{2}{5}x \right) = \frac{{35x}^{2}- 1}{5}
{-35x}^{2}:5 + (\left(\frac{2}{5} \right)x + \frac{1}{5})
{-7x}^{2} + (\left(\frac{2}{5} \right)x + \frac{1}{5})
\left(2:5*2:5 -4*(-7)*(1:5)\right)
4:25 -4*(-7:5)
\left(\frac{4}{25} \right)+\left(\frac{28}{5} \right)
\sqrt{\frac{140}{25}}
\left(\frac{2\sqrt[]{35}}{5} \right)
\left(\frac{\left-(\frac{2}{5} \right)x + \left(\frac{2\sqrt[]{35}}{5} \right)}{-14}\right)
\left(\frac{\left-(\frac{2}{5} \right)x - \left(\frac{2\sqrt[]{35}}{5} \right)}{-14}\right)](/latexrender/pictures/31bbfed4344375ec3c65b39e30099bf1.png)

![\sqrt[5]{{3}^{2x}} = {2.187}^{\frac{{35x}^{2}-1}{35}}
{\left({3}^{\frac{2}{3}} \right)}^{x} = 7*\left(\frac{{35x}^{2}-1}{35} \right)
\left(\frac{2}{5}x \right) = \frac{{245x}^{2}- 7}{35}
\left(\frac{2}{5}x \right) = \frac{{35x}^{2}- 1}{5}
{-35x}^{2}:5 + (\left(\frac{2}{5} \right)x + \frac{1}{5})
{-7x}^{2} + (\left(\frac{2}{5} \right)x + \frac{1}{5})
\left(2:5*2:5 -4*(-7)*(1:5)\right)
4:25 -4*(-7:5)
\left(\frac{4}{25} \right)+\left(\frac{28}{5} \right)
\sqrt{\frac{140}{25}}
\left(\frac{2\sqrt[]{35}}{5} \right)
\left(\frac{\left-(\frac{2}{5} \right)x + \left(\frac{2\sqrt[]{35}}{5} \right)}{-14}\right)
\left(\frac{\left-(\frac{2}{5} \right)x - \left(\frac{2\sqrt[]{35}}{5} \right)}{-14}\right) \sqrt[5]{{3}^{2x}} = {2.187}^{\frac{{35x}^{2}-1}{35}}
{\left({3}^{\frac{2}{3}} \right)}^{x} = 7*\left(\frac{{35x}^{2}-1}{35} \right)
\left(\frac{2}{5}x \right) = \frac{{245x}^{2}- 7}{35}
\left(\frac{2}{5}x \right) = \frac{{35x}^{2}- 1}{5}
{-35x}^{2}:5 + (\left(\frac{2}{5} \right)x + \frac{1}{5})
{-7x}^{2} + (\left(\frac{2}{5} \right)x + \frac{1}{5})
\left(2:5*2:5 -4*(-7)*(1:5)\right)
4:25 -4*(-7:5)
\left(\frac{4}{25} \right)+\left(\frac{28}{5} \right)
\sqrt{\frac{140}{25}}
\left(\frac{2\sqrt[]{35}}{5} \right)
\left(\frac{\left-(\frac{2}{5} \right)x + \left(\frac{2\sqrt[]{35}}{5} \right)}{-14}\right)
\left(\frac{\left-(\frac{2}{5} \right)x - \left(\frac{2\sqrt[]{35}}{5} \right)}{-14}\right)](/latexrender/pictures/31bbfed4344375ec3c65b39e30099bf1.png)








 , por exemplo, a equação ficaria
, por exemplo, a equação ficaria  . Basicamente o que eu fiz foi multiplicar os dois lados por 5, eliminando o denominador em comum.
. Basicamente o que eu fiz foi multiplicar os dois lados por 5, eliminando o denominador em comum.

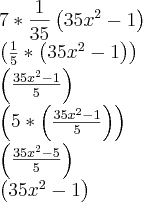

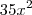 por 5 na penúltima linha.
por 5 na penúltima linha.


 pois
pois  .
.
