 por rita becher » Seg Mai 16, 2011 14:33
por rita becher » Seg Mai 16, 2011 14:33
Estou com dificuldade em alguma iuntegrais por substituição:
a)
![[tex]\int x(1-4)^4 dx = 1/6(1-x)^6 -1/5(1-x)^5 + c
b) [tex][tex]\int3x(2-x)^6dx=-6/7(2-x)^7+3/8(2-x)^8 +c
c)[tex][tex]\int(x^2/(x^2+4))dx=x-2arctag(x/2) + c [tex]\int x(1-4)^4 dx = 1/6(1-x)^6 -1/5(1-x)^5 + c
b) [tex][tex]\int3x(2-x)^6dx=-6/7(2-x)^7+3/8(2-x)^8 +c
c)[tex][tex]\int(x^2/(x^2+4))dx=x-2arctag(x/2) + c](/latexrender/pictures/35c3d850ad7527775f045da4ba778bfe.png)
[/tex]
Faz algun tempo que não uso, preciso de ajuda para relembrar. Obrigado
-
rita becher
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Mai 15, 2011 19:18
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielFerreira » Dom Mar 04, 2012 10:35
por DanielFerreira » Dom Mar 04, 2012 10:35
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integrais] Substituição
por dehcalegari » Qua Ago 07, 2013 09:34
- 2 Respostas
- 1015 Exibições
- Última mensagem por dehcalegari

Qua Ago 07, 2013 12:52
Cálculo: Limites, Derivadas e Integrais
-
- Integrais por substituição
por jeff_95 » Dom Dez 01, 2013 17:04
- 1 Respostas
- 996 Exibições
- Última mensagem por e8group

Dom Dez 01, 2013 17:16
Cálculo: Limites, Derivadas e Integrais
-
- [Integrais] Método da substituição
por Gabriel_1403 » Sáb Set 29, 2012 14:50
- 1 Respostas
- 1566 Exibições
- Última mensagem por MarceloFantini

Sáb Set 29, 2012 15:26
Cálculo: Limites, Derivadas e Integrais
-
- Integrais por substituição trigonométrica
por Victor Mello » Seg Nov 11, 2013 23:13
- 3 Respostas
- 1858 Exibições
- Última mensagem por Victor Mello

Ter Nov 12, 2013 23:32
Cálculo: Limites, Derivadas e Integrais
-
- [Usando tecnicas de integrais por substituiçao simples]
por menino de ouro » Qua Out 24, 2012 23:10
- 1 Respostas
- 1682 Exibições
- Última mensagem por MarceloFantini

Qui Out 25, 2012 01:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![[tex]\int x(1-4)^4 dx = 1/6(1-x)^6 -1/5(1-x)^5 + c
b) [tex][tex]\int3x(2-x)^6dx=-6/7(2-x)^7+3/8(2-x)^8 +c
c)[tex][tex]\int(x^2/(x^2+4))dx=x-2arctag(x/2) + c [tex]\int x(1-4)^4 dx = 1/6(1-x)^6 -1/5(1-x)^5 + c
b) [tex][tex]\int3x(2-x)^6dx=-6/7(2-x)^7+3/8(2-x)^8 +c
c)[tex][tex]\int(x^2/(x^2+4))dx=x-2arctag(x/2) + c](/latexrender/pictures/35c3d850ad7527775f045da4ba778bfe.png) [/tex]
[/tex]
![[tex]\int x(1-4)^4 dx = 1/6(1-x)^6 -1/5(1-x)^5 + c
b) [tex][tex]\int3x(2-x)^6dx=-6/7(2-x)^7+3/8(2-x)^8 +c
c)[tex][tex]\int(x^2/(x^2+4))dx=x-2arctag(x/2) + c [tex]\int x(1-4)^4 dx = 1/6(1-x)^6 -1/5(1-x)^5 + c
b) [tex][tex]\int3x(2-x)^6dx=-6/7(2-x)^7+3/8(2-x)^8 +c
c)[tex][tex]\int(x^2/(x^2+4))dx=x-2arctag(x/2) + c](/latexrender/pictures/35c3d850ad7527775f045da4ba778bfe.png) [/tex]
[/tex]

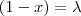
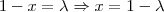

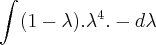
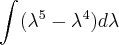
![\left[\frac{\lambda^6}{6} - \frac{\lambda^5}{5}\right] + c \left[\frac{\lambda^6}{6} - \frac{\lambda^5}{5}\right] + c](/latexrender/pictures/4975f9bbdbc822296fc922cfbfaef799.png)
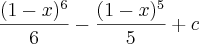


 .
.



