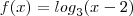
DADOS OS VALORES PARA x :
a)Se x=-2
b)Se x=-1
c)Se x=1
d)Se x=0
Detalhe as resposta são:
a)=

b)=

c)=

d)=

Agradeço muito quem resolver esse calculo

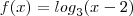








 , pois 3 elevado a nenhum número vai ter como resultado -2.
, pois 3 elevado a nenhum número vai ter como resultado -2. ... Coloque a questão como está no livro ou então tire uma foto dela e coloque aqui.
... Coloque a questão como está no livro ou então tire uma foto dela e coloque aqui.

 definida por
definida por  e
e 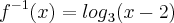
 no mesmo plano.
no mesmo plano.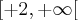

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.
 :
: