 por Vanessa_Dias » Sex Abr 15, 2011 23:49
por Vanessa_Dias » Sex Abr 15, 2011 23:49
Questão - A poligonal ABCD da figura adiante (é só a primeira figura, a que tem um gráfico) é o gráfico de uma função f cujo o domínio é o intervalo -1
< x
< 7. Sabe-se que AB é paralelo a CD e BC é paralelo ao eixo do x.
Essa é a imagem:
http://htmlimg1.scribdassets.com/6musdh ... ef/000.jpgNessas condições, f(7)-f(4,5) é igual a:
a) 3/2 b) 5/3 c) 17/10 d) 9/5 e)2
Resp.: b) 5/3
Eu to tentando por sistema, mas os resultados sempre dão diferentes, não sei como achar a função.
Me ajudem, por farvor!
-
Vanessa_Dias
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Abr 15, 2011 23:08
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Sáb Abr 16, 2011 01:31
por MarceloFantini » Sáb Abr 16, 2011 01:31
Se

, então o coeficiente angular de AB é igual ao coeficiente de CD. Assim,
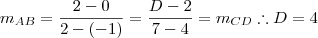
Logo,
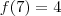
. Para encontrarmos
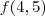
, basta pegar o coeficiente angular e fazer uma variação de meio no denominador:
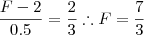
Portanto,
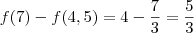
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por FilipeCaceres » Sáb Abr 16, 2011 01:32
por FilipeCaceres » Sáb Abr 16, 2011 01:32
Observe que como AB é paralelo a CD, então ambos tem o mesmo coeficiente angular, logo:
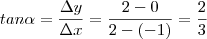
Montanto a função temos:

Do ponto C(4,2) tiraremos o valor de b
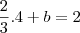
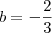
Assim temos,

Logo,
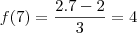
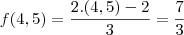
Portanto,


Espero ter ajudado.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por FilipeCaceres » Sáb Abr 16, 2011 14:16
por FilipeCaceres » Sáb Abr 16, 2011 14:16

Abraço
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Vanessa_Dias » Dom Abr 17, 2011 16:43
por Vanessa_Dias » Dom Abr 17, 2011 16:43
Obrigada, gente!
Mas só tem como responder por essa fórmula?
-
Vanessa_Dias
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Abr 15, 2011 23:08
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Dom Abr 17, 2011 16:48
por MarceloFantini » Dom Abr 17, 2011 16:48
Isso não é uma fórmula, isso é a definição de coeficiente angular, ou seja, inclinação da reta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- duvida em uma questão da vunesp
 por juliacajango » Qua Jun 13, 2012 17:17
por juliacajango » Qua Jun 13, 2012 17:17
- 1 Respostas
- 2633 Exibições
- Última mensagem por LuizAquino

Qua Jun 13, 2012 20:15
Geometria Analítica
-
- VUNESP
por DanielFerreira » Seg Fev 28, 2011 09:49
- 2 Respostas
- 8253 Exibições
- Última mensagem por DanielFerreira

Seg Fev 28, 2011 11:01
Progressões
-
- ( Vunesp )
por my2009 » Sex Jul 29, 2011 12:18
- 1 Respostas
- 1063 Exibições
- Última mensagem por Molina

Sex Jul 29, 2011 16:21
Funções
-
- Trigonometria (Vunesp-SP)
 por Karina » Qui Jul 22, 2010 17:51
por Karina » Qui Jul 22, 2010 17:51
- 5 Respostas
- 9591 Exibições
- Última mensagem por Douglasm

Sáb Jul 24, 2010 22:26
Trigonometria
-
- (VUNESP-SP) Função
por Rafael16 » Ter Mar 13, 2012 21:11
- 3 Respostas
- 6150 Exibições
- Última mensagem por Russman

Qui Jun 21, 2012 17:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , então o coeficiente angular de AB é igual ao coeficiente de CD. Assim,
, então o coeficiente angular de AB é igual ao coeficiente de CD. Assim, 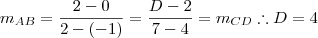
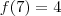 . Para encontrarmos
. Para encontrarmos 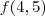 , basta pegar o coeficiente angular e fazer uma variação de meio no denominador:
, basta pegar o coeficiente angular e fazer uma variação de meio no denominador: 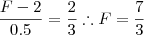
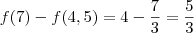


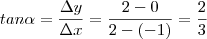

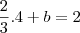
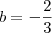

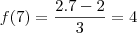
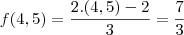




 .
.



