Função de segundo grau simples
Opa pessoal beleza? Comecei a ler a série "Fundamentos da Matemática Elementar". Ainda no primeiro volume estou tendo problemas com o exercicio A177 letra J que é o seguinte  , enquanto calculava o delta cheguei nisso:
, enquanto calculava o delta cheguei nisso:
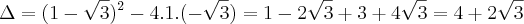
isso me pareceu bem estranho, imaginei que o delta não possuiria nenhuma raiz quadrada, a equação toda ficaria assim:
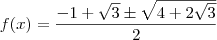
Os resultados seriam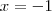 e
e 
Acredito ter errado em alguma coisa bem boba, mas não consigo identificá-la. Obrigado pela ajuda.
PS: Primeira vez usando o LaTex então talvez alguma coisa na fórmula não tenha ficado como deveria.
 , enquanto calculava o delta cheguei nisso:
, enquanto calculava o delta cheguei nisso: 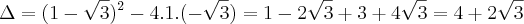
isso me pareceu bem estranho, imaginei que o delta não possuiria nenhuma raiz quadrada, a equação toda ficaria assim:
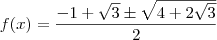
Os resultados seriam
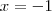 e
e 
Acredito ter errado em alguma coisa bem boba, mas não consigo identificá-la. Obrigado pela ajuda.
PS: Primeira vez usando o LaTex então talvez alguma coisa na fórmula não tenha ficado como deveria.

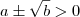
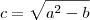 seja racional,temos:
seja racional,temos: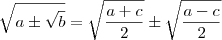
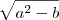 não for racional.
não for racional.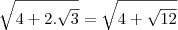

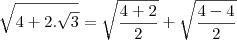
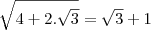

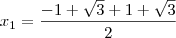



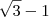 e multiplicados
e multiplicados 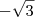 ? Fica um tanto quanto nítido. Não sei ele já ensinou isso, portanto talvez desconsidere. O caso é que eu acho que esse método pelo tal "radical duplo" é usar um canhão para matar uma formiga. Acho específico demais (pessoalmente nunca vi isso em nenhuma prova, vestibular, livro de ensino médio ou matéria da universidade) para ser usado num único problema. Deve existir um outro jeito de visualizar, possivelmente sem ser o meu ou do radical, de forma mais natural e sem uso de tal artifício.
? Fica um tanto quanto nítido. Não sei ele já ensinou isso, portanto talvez desconsidere. O caso é que eu acho que esse método pelo tal "radical duplo" é usar um canhão para matar uma formiga. Acho específico demais (pessoalmente nunca vi isso em nenhuma prova, vestibular, livro de ensino médio ou matéria da universidade) para ser usado num único problema. Deve existir um outro jeito de visualizar, possivelmente sem ser o meu ou do radical, de forma mais natural e sem uso de tal artifício. . Desse modo, temos que
. Desse modo, temos que 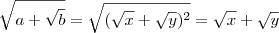 .
.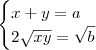

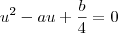
 . Nesse caso, as soluções serão:
. Nesse caso, as soluções serão:  e
e  .
.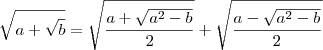
 , chegamos na relação:
, chegamos na relação:
 for racional. Se isso fosse irracional, teríamos que
for racional. Se isso fosse irracional, teríamos que  para algum
para algum 
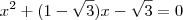 , o caminho mais simples é mesmo analisar a soma e o produto das raízes.
, o caminho mais simples é mesmo analisar a soma e o produto das raízes. . Duas raízes para essa equação são
. Duas raízes para essa equação são 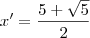 e
e  . Note que seria difícil ter chegado nessa solução usando a estratégia de analisar a soma e o produto das raízes. Entretanto, usando a estratégia acima podemos chegar nesse resultado.
. Note que seria difícil ter chegado nessa solução usando a estratégia de analisar a soma e o produto das raízes. Entretanto, usando a estratégia acima podemos chegar nesse resultado. e
e  .
. para transformá-lo em
para transformá-lo em  .
.