por ficotolo » Dom Nov 14, 2010 16:34
Ja tou um bocado enferrujado com funçoes, ainda por cima esta é um bocado complicada (pelo menos para mim)
Preciso de ajuda no estudo desta função:
f(x)=
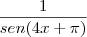
Até agora cheguei a conclusão que:
- Domínio é |R \ {
}
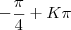
- Contra dominio =
]-?-1] ? [1, +?]- Não tem zeros. (equaçao deu impossível)
- É ímpar. ( provei que
)
- Período é
- Não tem função inversa (pq não é injectiva)
Falta me ver:
Se é ou não continua, se é diferenciavel, ver os intervalos de monotonia, os extremos, o sentido de concavidade, e as assimptotas.
E um exemplo dum problema da 'vida real' para esta função ...
Tenho de provar tudo com cálculos...
Agradeço qualquer correcção/explicação/ajuda em qualquer um destes tópicos, é um bocado urgente ...
-
ficotolo
- Novo Usuário
-
- Mensagens: 1
- Registrado em: Dom Nov 14, 2010 16:14
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Números inteiros no intervalo duma função]
por Jhenrique » Dom Ago 26, 2012 20:33
- 1 Respostas
- 1423 Exibições
- Última mensagem por Jhenrique
Qua Set 26, 2012 04:21
Funções
-
- Função Racional - preciso de ajuda para hoje ainda!
por raf » Seg Set 28, 2015 14:32
- 1 Respostas
- 2493 Exibições
- Última mensagem por nakagumahissao
Sex Out 02, 2015 00:47
Funções
-
- Estudo da função
por Harzeus » Seg Jan 10, 2011 13:58
- 1 Respostas
- 1086 Exibições
- Última mensagem por Neperiano
Qui Out 27, 2011 15:27
Funções
-
- Função ( Estudo do sinal )
por clara » Dom Jun 21, 2009 20:55
- 1 Respostas
- 5219 Exibições
- Última mensagem por Molina
Seg Jun 22, 2009 12:57
Funções
-
- Estudo de uma Função Logaritmica
por Ice » Dom Jul 24, 2011 18:06
- 3 Respostas
- 1605 Exibições
- Última mensagem por LuizAquino
Dom Jul 24, 2011 21:30
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
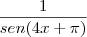
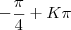