vou ter uma prova sexta feira, e preciso de ajuda!
Alguem pode me passar exercicios de função de 2° grau, oque pode cair em prova etc... to aprendendo isso...
Estudo do sinal e inequação do 2° grau
Estudar o sinal de cada função
f(x) = -3x² + 2x + 1
[...] fazer a reta real, por as 2 raizes, e escrever as soluções
f(x) = 0 se x ....
f(x) < 0 se ...
f(x) >0 se x...
E então vem inequação de 2° grau
y = x² - 3x + 2
 0
0entao resolvo com bhaskara, achando as 2 raizes, fazendo o "varalzinho" na parte que é pedido, e escrevendo a solução S=[xer/x<....>..]
Entao pessoal, é +/- isso que estou aprendendo nessa parte, sera que algum pode me passar uns exercicios, doqe pode cair de mais dificl na prova, dicas, etc... ?
vlw ae


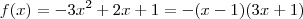
 e
e  , ou seja,
, ou seja,  se anula quando
se anula quando  for 1 ou
for 1 ou 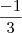 .
. é negativo que é uma parábola com a boca para baixo. Assim, entre as raízes a função é positiva, e fora desse intervalo é negativa.
é negativo que é uma parábola com a boca para baixo. Assim, entre as raízes a função é positiva, e fora desse intervalo é negativa.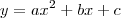 , com
, com  , o que isso quer dizer? Você está tomando os pontos da curva dada. Se
, o que isso quer dizer? Você está tomando os pontos da curva dada. Se 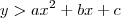 , você está tomando os pontos ACIMA da curva, sem incluí-los (incluindo-os seria com um maior ou igual). Analogamente,
, você está tomando os pontos ACIMA da curva, sem incluí-los (incluindo-os seria com um maior ou igual). Analogamente, 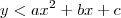 quer dizer os pontos abaixo da curva.
quer dizer os pontos abaixo da curva.



 , avisa que eu resolvo.
, avisa que eu resolvo.

