OLá!!
Não estou conseguindo resolver estas questões. Não estou conseguindo interpretar os encunciados. Não sei como se faz para resolver. Se alguem puder me mostrar como se interpreta e como devo resolve-las! Desde já agradeço a ajuda
1)Represente geometricamente as seguintes relações no plano cartesiano:
R1 = { (x,y) ? R x R / |X| + | Y| ? 1}
R2 = { (x,y) ? R x R |/ X² + Y² ? 1}
R3 = { (x,y) ? R x R / Max { |X| , | Y| ? 1}
2) Determine o domínio e imagem das relações definidas acima e prove analiticamente que R1 está contido R2.
Algumas dessas relações e simétrica, reflexiva, ou transitiva?
3) Determine a imagem da relação R definida por
R = { (x,y) ? R x R | y| ? x² - 4x +7}
e represente geometricamente R (elevado na menos 1). Dê a imagem de R (elevado na menos 1.


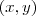 é a representação de um par ordenado, um ponto genérico no plano cartesiano.
é a representação de um par ordenado, um ponto genérico no plano cartesiano.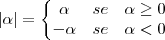
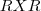 representa o plano cartesiano em duas dimensões (
representa o plano cartesiano em duas dimensões ( ).
).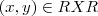 significa um ponto do plano.
significa um ponto do plano.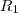 :
: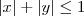 .
.

 .
.
 :
: