 por Striker694 » Qui Jun 30, 2016 23:30
por Striker694 » Qui Jun 30, 2016 23:30
Alguém poderia me ajudar urgente com esse problema, por favor?
O volume "v", em centímetro cúbico de um corpo, varia em função da temperatura "t" em graus Celsius, de acordo com a função
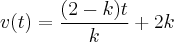
, sendo k uma constante real não nula. Para que valores de k a taxa de variação dessa função é positiva?
-
Striker694
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Jun 30, 2016 23:13
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: curso técnico em informática
- Andamento: cursando
 por adauto martins » Qui Jul 07, 2016 11:49
por adauto martins » Qui Jul 07, 2016 11:49

...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função simples (UFF-RJ)
por guijermous » Ter Fev 16, 2010 12:08
- 2 Respostas
- 1898 Exibições
- Última mensagem por guijermous

Ter Fev 16, 2010 12:40
Funções
-
- Função simples
por Pad » Ter Jul 10, 2012 20:30
- 1 Respostas
- 3840 Exibições
- Última mensagem por Russman

Ter Jul 10, 2012 21:39
Funções
-
- Função simples
por esdraslima » Sáb Jul 09, 2016 02:00
- 1 Respostas
- 2202 Exibições
- Última mensagem por DanielFerreira

Sáb Jul 09, 2016 12:32
Funções
-
- função simples de derivada
por miumatos » Dom Mar 18, 2012 13:06
- 2 Respostas
- 2252 Exibições
- Última mensagem por miumatos

Dom Mar 18, 2012 15:29
Cálculo: Limites, Derivadas e Integrais
-
- [Função Simples] Comparando f(x) e g(x)
por Rike Morais » Sex Jul 08, 2016 16:41
- 3 Respostas
- 3029 Exibições
- Última mensagem por Daniel Bosi

Sex Jul 08, 2016 17:44
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
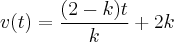 , sendo k uma constante real não nula. Para que valores de k a taxa de variação dessa função é positiva?
, sendo k uma constante real não nula. Para que valores de k a taxa de variação dessa função é positiva?
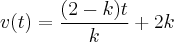 , sendo k uma constante real não nula. Para que valores de k a taxa de variação dessa função é positiva?
, sendo k uma constante real não nula. Para que valores de k a taxa de variação dessa função é positiva?


 .
.
 :
: