 por Mimizinha » Ter Abr 01, 2008 10:27
por Mimizinha » Ter Abr 01, 2008 10:27
Um produto deve ser colocado no mercado a um preço de venda mínimo de R$5,00. O fabricante acredita que a cada aumento no preço do produto, a partir do preço mínimo, ele perca consumidor a uma taxa de 1000 para cada real aumentado. O mercado estimadoara o preço mínimo e de 10.000 unidades. A quantidade mínima que interessa para os fornecedores e 1000 unidades, pois abaixo disso há outras atividades mais rentáveis disponíveis. Contruir um modelo funcional para a quantidade vendida do produto a cada nível de preço
Por favor me ajude a resolver esse exercicio. Não faço a minima ideia nem de como começar
Obrigada
-
Mimizinha
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Qua Mar 19, 2008 13:50
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Ter Abr 01, 2008 11:38
por admin » Ter Abr 01, 2008 11:38
Olá.
Comece pensando na quantidade vendida como uma função do preço.
Durante sua reflexão, veja como a quantidade vendida começa e como ela varia conforme o preço aumenta.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Mimizinha » Ter Abr 01, 2008 15:13
por Mimizinha » Ter Abr 01, 2008 15:13
ainda não consegui chegar a esse raciocionio que vc disse
-
Mimizinha
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Qua Mar 19, 2008 13:50
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Ter Abr 01, 2008 23:59
por admin » Ter Abr 01, 2008 23:59
Olá.
Então, tente identificar no problema uma função de 1º grau.
Ou seja, estando

em função de

, identifique

e

, assim como os parâmetros

e

:
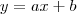
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [idades] ajuda na resolução de exercicio
por Mimizinha » Qui Mar 20, 2008 14:14
- 7 Respostas
- 7176 Exibições
- Última mensagem por admin

Qua Mar 26, 2008 11:59
Álgebra Elementar
-
- [Cálculo I] Ajuda na resolução de um exercício
por dehcalegari » Qui Abr 04, 2013 09:24
- 1 Respostas
- 2016 Exibições
- Última mensagem por young_jedi

Qui Abr 04, 2013 19:48
Cálculo: Limites, Derivadas e Integrais
-
- Exercício de função para ajuda na resolução.
 por MARCION » Seg Dez 15, 2014 13:31
por MARCION » Seg Dez 15, 2014 13:31
- 3 Respostas
- 2314 Exibições
- Última mensagem por Russman

Seg Dez 15, 2014 19:56
Funções
-
- Resolução de exercício
 por Flavia Araujo » Qui Mai 21, 2009 14:38
por Flavia Araujo » Qui Mai 21, 2009 14:38
- 28 Respostas
- 35701 Exibições
- Última mensagem por Neperiano

Ter Fev 23, 2010 13:50
Progressões
-
- resolução de exercício
 por jose henrique » Sex Nov 12, 2010 21:20
por jose henrique » Sex Nov 12, 2010 21:20
- 2 Respostas
- 2425 Exibições
- Última mensagem por MarceloFantini

Sex Nov 12, 2010 22:58
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 em função de
em função de  , identifique
, identifique  e
e  :
: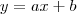


 , avisa que eu resolvo.
, avisa que eu resolvo.

