 por Cleyson007 » Dom Abr 03, 2016 16:46
por Cleyson007 » Dom Abr 03, 2016 16:46
Boa tarde Ana Carolina!
Seja muito bem-vinda ao nosso fórum.
Estou tendo dificuldade para entender o que você digitou no LaTeX.. Será isso?
![\frac{\sqrt[6]{5x^2*5x^3*5x^2*5x^3}}{\sqrt[3]{5x^2}}\,x^2*x^2 \frac{\sqrt[6]{5x^2*5x^3*5x^2*5x^3}}{\sqrt[3]{5x^2}}\,x^2*x^2](/latexrender/pictures/76c98c9e178c48acb51a9e3ee532449a.png)
A diferença é que troquei a incógnita "A" por x.
Aguardo seu comentário para poder lhe ajudar.
Att,
Prof° Clésio
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Ana29Carolina » Qua Abr 06, 2016 12:24
por Ana29Carolina » Qua Abr 06, 2016 12:24
Olá ! Muito obrigada ! Tive muita dificuldade em escrever no Latex. Na verdade, não há incógnitas e o 5 da primeira raíz é elevado por 10. E o resultado da divisão das raízes é elevado a 4. Você conseguiu entender ? Desde já, completamente agradecida !
-
Ana29Carolina
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Mar 29, 2016 16:11
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudante
- Andamento: cursando
 por Cleyson007 » Qui Abr 07, 2016 10:30
por Cleyson007 » Qui Abr 07, 2016 10:30
Olá, bom dia!
É um prazer ajudar

Ainda não consegui entender

Você consegue anexar um arquivo no tópico? Caso consiga, favor escanear a questão escrita e me envie por favor.
Uma forma alternativa é me contactar pelo WhatsApp: (38) 9889-5755.
Att,
Prof° Clésio
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Ana29Carolina » Qui Abr 07, 2016 17:10
por Ana29Carolina » Qui Abr 07, 2016 17:10
Aqui está o anexo da radiciação com potenciação e divisão. Veja ! Desde já, muito obrigada! =)
- Anexos
-

- Radiciação com divisão
- 1.PNG (16.02 KiB) Exibido 3354 vezes
-
Ana29Carolina
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Mar 29, 2016 16:11
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudante
- Andamento: cursando
 por Cleyson007 » Sex Abr 08, 2016 12:35
por Cleyson007 » Sex Abr 08, 2016 12:35
Bom dia Ana Carolina!
Está ok. Vamos lá?
![\sqrt[6]{{5}^{10}} \sqrt[6]{{5}^{10}}](/latexrender/pictures/1d5f337d64ce1a916b7784181a2372fd.png)
pode ser escrito como

. E,
![\sqrt[3]{{5}^{2}} \sqrt[3]{{5}^{2}}](/latexrender/pictures/b45814079ccc448a173556f262472704.png)
pode ser escrito como

.
Juntando essas informações, temos que:
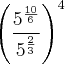
Dentro do parênteses temos uma divisão de mesma base e, a regra diz que devemos conservar essa base (5) e subtrair os seus expoentes. Logo,
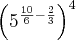

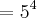

Qualquer dúvida estou a disposição.
Att,
Prof° Clésio
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Ana29Carolina » Sex Abr 08, 2016 14:34
por Ana29Carolina » Sex Abr 08, 2016 14:34
Cheguei ao mesmo resultado, porém a folha diz que a resposta é
![5\sqrt[3]{5} 5\sqrt[3]{5}](/latexrender/pictures/67f83f1201f3d8c9d34e70b09ae53de6.png)
.
-
Ana29Carolina
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Mar 29, 2016 16:11
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudante
- Andamento: cursando
 por Ana29Carolina » Qui Mai 05, 2016 11:40
por Ana29Carolina » Qui Mai 05, 2016 11:40
Você poderia me ajudar a chegar nesse resultado já dito acima, por favor ?

-
Ana29Carolina
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Mar 29, 2016 16:11
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudante
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Definição de Multiplicação/Divisão/Potênciação/Radiciação
por Jhenrique » Sex Nov 02, 2012 11:17
- 1 Respostas
- 1240 Exibições
- Última mensagem por MarceloFantini

Sex Nov 02, 2012 12:11
Álgebra Elementar
-
- Potenciação e Radiciação
por Carlos22 » Qua Abr 13, 2011 22:06
- 1 Respostas
- 1917 Exibições
- Última mensagem por FilipeCaceres

Qua Abr 13, 2011 22:27
Logaritmos
-
- [Potenciação e radiciação]
por SCHOOLGIRL+T » Qua Nov 07, 2012 21:19
- 4 Respostas
- 2652 Exibições
- Última mensagem por SCHOOLGIRL+T

Sex Nov 09, 2012 23:44
Álgebra Elementar
-
- [Potenciação e Radiciação]
por JU201015 » Seg Nov 12, 2012 22:06
- 2 Respostas
- 1937 Exibições
- Última mensagem por JU201015

Ter Nov 13, 2012 09:08
Álgebra Elementar
-
- Potenciação e radiciação
por anneliesero » Sáb Abr 27, 2013 22:46
- 1 Respostas
- 1651 Exibições
- Última mensagem por e8group

Sáb Abr 27, 2013 23:48
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![(\sqrt[6]{5²*5³*5²*5³}/\sqrt[3]{5²})²*² (\sqrt[6]{5²*5³*5²*5³}/\sqrt[3]{5²})²*²](/latexrender/pictures/8ffd2f8042da61573ad34e34c7018f03.png)
 , porém não consegui chegar nele. Se puderem me ajudar, serei completamente agradecida !
, porém não consegui chegar nele. Se puderem me ajudar, serei completamente agradecida !
![(\sqrt[6]{5²*5³*5²*5³}/\sqrt[3]{5²})²*² (\sqrt[6]{5²*5³*5²*5³}/\sqrt[3]{5²})²*²](/latexrender/pictures/8ffd2f8042da61573ad34e34c7018f03.png)
 , porém não consegui chegar nele. Se puderem me ajudar, serei completamente agradecida !
, porém não consegui chegar nele. Se puderem me ajudar, serei completamente agradecida !
![\frac{\sqrt[6]{5x^2*5x^3*5x^2*5x^3}}{\sqrt[3]{5x^2}}\,x^2*x^2 \frac{\sqrt[6]{5x^2*5x^3*5x^2*5x^3}}{\sqrt[3]{5x^2}}\,x^2*x^2](/latexrender/pictures/76c98c9e178c48acb51a9e3ee532449a.png)






![\sqrt[6]{{5}^{10}} \sqrt[6]{{5}^{10}}](/latexrender/pictures/1d5f337d64ce1a916b7784181a2372fd.png) pode ser escrito como
pode ser escrito como  . E,
. E, ![\sqrt[3]{{5}^{2}} \sqrt[3]{{5}^{2}}](/latexrender/pictures/b45814079ccc448a173556f262472704.png) pode ser escrito como
pode ser escrito como  .
.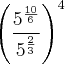
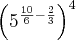

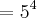


![5\sqrt[3]{5} 5\sqrt[3]{5}](/latexrender/pictures/67f83f1201f3d8c9d34e70b09ae53de6.png) .
.

